题目内容
(本小题满分13分)已知四棱锥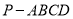 中,
中,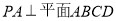 ,底面
,底面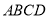 是边长为
是边长为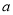 的菱形,
的菱形,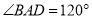 ,
,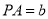 .
.
(Ⅰ)求证: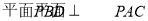 ;
;
(Ⅱ)设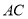 与
与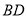 交于点
交于点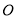 ,
,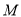 为
为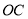 中点,若二面角
中点,若二面角 的正切值为
的正切值为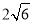 ,求
,求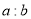 的值.
的值.
(1)证明见解析;(2)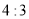 .
.
【解析】
试题分析:(1)利用面面垂直的判定定理进行证明;(2)建立空间直角坐标系,利用空间向量进行求解.
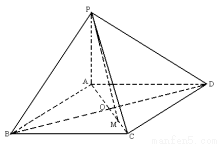
试题解析:(Ⅰ)因为PA⊥平面ABCD,所以PA⊥BD又ABCD为菱形,所以AC⊥BD,所以BD⊥平面PAC从而平面PBD⊥平面PAC.
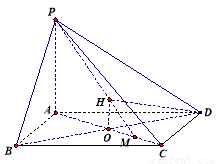
(Ⅱ)方法1.过O作OH⊥PM交PM于H,连HD
因为DO⊥平面PAC,可以推出DH⊥PM,所以∠OHD为O-PM-D的平面角 8分
又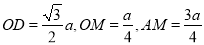 ,且
,且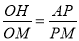 10分
10分
从而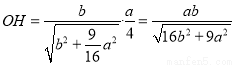 12分
12分
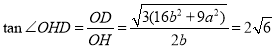
所以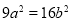 ,即
,即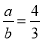 . 13分
. 13分
法二:如图,以 为原点,
为原点,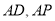 所在直线为
所在直线为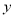 轴,
轴,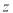 轴建立空间直角坐标系,
轴建立空间直角坐标系,
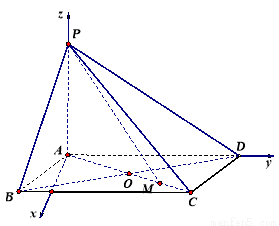
则 ,
,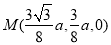 ,
,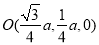 8分
8分
从而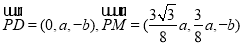
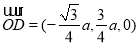 9分
9分
因为BD⊥平面PAC,所以平面PMO的一个法向量为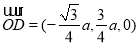 . 10分
. 10分
设平面PMD的法向量为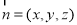 ,由
,由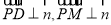 得
得
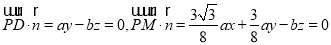
取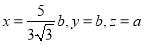 ,即
,即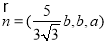 11分
11分
设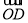 与
与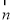 的夹角为
的夹角为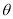 ,则二面角
,则二面角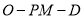 大小与
大小与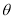 相等
相等
从而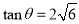 ,得
,得
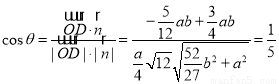
从而 ,即
,即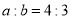 .
.
考点:1.面面垂直的判定定理;2.二面角;3.空间向量的应用.
考点分析: 考点1:空间向量与立体几何 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 、边长为
、边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
 平面PAD;
平面PAD; 的四个命题:
的四个命题: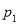 :
: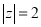 ,
, 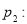
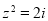
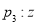 的共轭复数为
的共轭复数为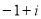
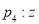 的虚部为
的虚部为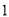
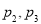 B.
B.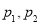 C.
C.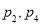 D.
D.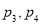
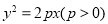 焦点为F,O为坐标原点,M为抛物线上一点,且
焦点为F,O为坐标原点,M为抛物线上一点,且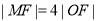 ,
,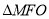 的面积为
的面积为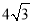 ,则抛物线方程为
,则抛物线方程为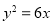 B.
B.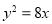 C.
C.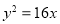 D.
D.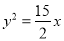
 的不等式:
的不等式: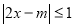 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.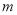 的值;
的值;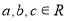 ,若
,若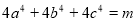 ,求
,求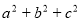 的最大值.
的最大值. 和等比数列
和等比数列 首项都是1,公差和公比都是2,则
首项都是1,公差和公比都是2,则 .
.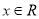 , 对于使
, 对于使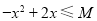 成立的所有常数
成立的所有常数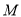 中,我们把
中,我们把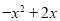 的上确界.若
的上确界.若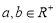 ,且
,且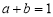 ,则
,则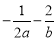 的上确界为
的上确界为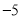 B.
B.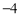 C.
C.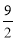 D.
D.
 的值域是( )
的值域是( ) B.
B. C.
C. D.
D.
 =_____.
=_____.