题目内容
已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )
(A)(0,2) (B)(0,8) (C)(2,8) (D)(-∞,0)
【答案】
B
【解析】当m≤0时,显然不成立,当m>0时,因f(0)=1>0,当-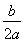
=
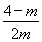≥0即0<m≤4时结论显然成立;
当-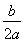=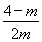<0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
练习册系列答案
相关题目