题目内容
已知椭圆C的中心在坐标原点,长轴在x轴上,F1、F2分别为其左、右焦点,P在椭圆上任意一点,且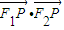 的最大值为1,最小值为-2.
的最大值为1,最小值为-2.(1)求椭圆C的方程;
(2)设A为椭圆C的右顶点,直线l是与椭圆交于M、N两点的任意一条直线,若AM⊥AN,证明直线l过定点.
【答案】分析:(1)设椭圆方程为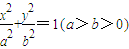 ,p(x,y)为椭圆上任意一点,
,p(x,y)为椭圆上任意一点,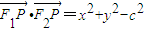 ,由
,由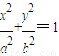 ,知
,知 =
= .由此能求出椭圆方程.
.由此能求出椭圆方程.
(2)①若直线l不垂直于x轴,设该直线方程为y=kx+m,M(x1,y1),N(x2,y2),由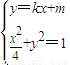 得x2+4(k2x2+2kmx+m2)=4,由此能求出
得x2+4(k2x2+2kmx+m2)=4,由此能求出 过定点(
过定点(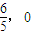 ).②若直线l垂直于x轴,设l与x轴交于点(x,0),由椭圆的对称性知△MNA为等腰Rt△,
).②若直线l垂直于x轴,设l与x轴交于点(x,0),由椭圆的对称性知△MNA为等腰Rt△,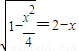 ,解得
,解得 此时直线l也过定点(
此时直线l也过定点(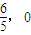 ).由此知,直线l恒过定点(
).由此知,直线l恒过定点(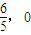 ).
).
解答:解:(1)设椭圆方程为 ,p(x,y)为椭圆上任意一点,
,p(x,y)为椭圆上任意一点,
∴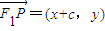 ,
,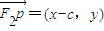 ,
,
∴ ,
,
∵ ,
,
∴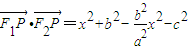 =
=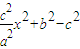 .
.
∵0≤x2≤a2,∴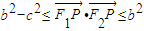 ,∴
,∴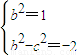 ,∴
,∴ ,∴a2=4,
,∴a2=4,
∴椭圆方程为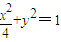 .
.
(2)①若直线l不垂直于x轴,设该直线方程为y=kx+m,M(x1,y1),N(x2,y2),
由 得x2+4(k2x2+2kmx+m2)=4,
得x2+4(k2x2+2kmx+m2)=4,
化简,得(1+4k2)x2+8kmx+4m2-4=0,∴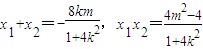 ,
,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=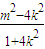 .
.
∵AM⊥AN,∴ ,
,
∴y1y2+x1x2-2(x1+x2)+4=0,
∴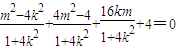 .整理,得12k2+16km+5m2=0,
.整理,得12k2+16km+5m2=0,
∴ 或
或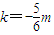 ,
,
当k=-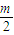 时,l:y=-
时,l:y=-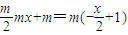 过定点(2,0),不满足题意.
过定点(2,0),不满足题意.
当 时,
时, 过定点(
过定点(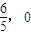 ).
).
②若直线l垂直于x轴,设l与x轴交于点(x,0),由椭圆的对称性知△MNA为等腰Rt△,
∴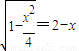 ,解得
,解得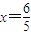 或2(舍),即此时直线l也过定点(
或2(舍),即此时直线l也过定点(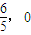 ).
).
由①②知,直线l恒过定点(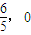 ).
).
点评:本题考查直线 和圆锥曲线的综合应用,具有一定的难度,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
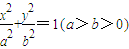 ,p(x,y)为椭圆上任意一点,
,p(x,y)为椭圆上任意一点,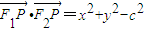 ,由
,由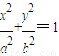 ,知
,知 =
= .由此能求出椭圆方程.
.由此能求出椭圆方程.(2)①若直线l不垂直于x轴,设该直线方程为y=kx+m,M(x1,y1),N(x2,y2),由
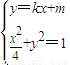 得x2+4(k2x2+2kmx+m2)=4,由此能求出
得x2+4(k2x2+2kmx+m2)=4,由此能求出 过定点(
过定点(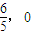 ).②若直线l垂直于x轴,设l与x轴交于点(x,0),由椭圆的对称性知△MNA为等腰Rt△,
).②若直线l垂直于x轴,设l与x轴交于点(x,0),由椭圆的对称性知△MNA为等腰Rt△,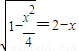 ,解得
,解得 此时直线l也过定点(
此时直线l也过定点(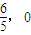 ).由此知,直线l恒过定点(
).由此知,直线l恒过定点(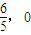 ).
).解答:解:(1)设椭圆方程为
 ,p(x,y)为椭圆上任意一点,
,p(x,y)为椭圆上任意一点,∴
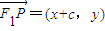 ,
,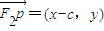 ,
,∴
 ,
,∵
 ,
,∴
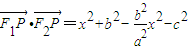 =
=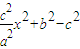 .
.∵0≤x2≤a2,∴
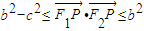 ,∴
,∴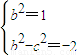 ,∴
,∴ ,∴a2=4,
,∴a2=4,∴椭圆方程为
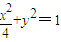 .
.(2)①若直线l不垂直于x轴,设该直线方程为y=kx+m,M(x1,y1),N(x2,y2),
由
 得x2+4(k2x2+2kmx+m2)=4,
得x2+4(k2x2+2kmx+m2)=4,化简,得(1+4k2)x2+8kmx+4m2-4=0,∴
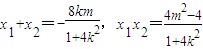 ,
,y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
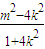 .
.∵AM⊥AN,∴
 ,
,∴y1y2+x1x2-2(x1+x2)+4=0,
∴
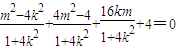 .整理,得12k2+16km+5m2=0,
.整理,得12k2+16km+5m2=0,∴
 或
或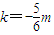 ,
,当k=-
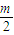 时,l:y=-
时,l:y=-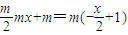 过定点(2,0),不满足题意.
过定点(2,0),不满足题意.当
 时,
时, 过定点(
过定点(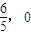 ).
).②若直线l垂直于x轴,设l与x轴交于点(x,0),由椭圆的对称性知△MNA为等腰Rt△,
∴
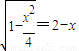 ,解得
,解得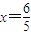 或2(舍),即此时直线l也过定点(
或2(舍),即此时直线l也过定点(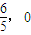 ).
).由①②知,直线l恒过定点(
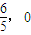 ).
).点评:本题考查直线 和圆锥曲线的综合应用,具有一定的难度,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,
已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,