题目内容
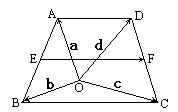
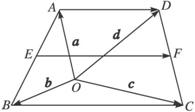
在梯形ABCD中，AB∥CD，且AB=2CD，E，F分别是AD，BC的中点．（1）若设
| AB |
| e1 |
| AD |
| e2 |
| e1 |
| e2 |
| EF |
| BC |
| CD |
| AC |
（2）若设
| EF |
| z1 |
| AC |
| z2 |
| z1 |
| z2 |
| AB |
| BC |
| CD |
| AD |
分析：（1）由
=
，
=
，结合AB∥CD，且AB=2CD，E，F分别是AD，BC的中点，结合向量加减法的三角形法则，我们易用
、
为基底表示
，
，
，
．
（2）由
=
，
=
，结合AB∥CD，且AB=2CD，E，F分别是AD，BC的中点，易（1）中向量间的关系，我们易用
，
为基底表示
，
，
，
．
| AB |
| e1 |
| AD |
| e2 |
| e1 |
| e2 |
| EF |
| BC |
| CD |
| AC |
（2）由
| EF |
| z1 |
| AC |
| z2 |
| z1 |
| z2 |
| AB |
| BC |
| CD |
| AD |
解答：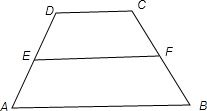
解：由图可得：
（1）若
=
，
=
，则
=
（
+
）=
=
，
=
+
+
=
-
=
-
，
=-
=-
，
=
+
=
+
=
+
．
（2）若
=
，
=
，则
=
=
，
=
+
=-
+
，
=-
=-
，
=
+
=
-
．
解：由图可得：（1）若
| AB |
| e1 |
| AD |
| e2 |
| EF |
| 1 |
| 2 |
| DC |
| AB |
| 3 |
| 4 |
| AB |
| 3 |
| 4 |
| e1 |
| BC |
| BA |
| AD |
| DC |
| AD |
| 1 |
| 2 |
| AB |
| e2 |
| 1 |
| 2 |
| e1 |
| CD |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| e1 |
| AC |
| AD |
| DC |
| AD |
| 1 |
| 2 |
| AB |
| e2 |
| 1 |
| 2 |
| e1 |
（2）若
| EF |
| z1 |
| AC |
| z2 |
| AB |
| 4 |
| 3 |
| EF |
| 4 |
| 3 |
| z1 |
| BC |
| BA |
| AC |
| 4 |
| 3 |
| z1 |
| z2 |
| CD |
| 1 |
| 2 |
| AB |
| 2 |
| 3 |
| z1 |
| AD |
| AC |
| CD |
| z2 |
| 2 |
| 3 |
| z1 |
点评：本题考查的知识点是平面向量的基本定理及其意义，根据平面图形的性质，结合平面向量加减法的三角形法则将各个向量分解为基底是解答本类问题的关键．
练习册系列答案
相关题目
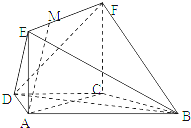如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
=a，
=b，
=c，
=d，E、F分别为AB、CD的中点，则下列表达中成立的是
=
(a＋b＋c＋d)
=a，
=b，
=c，
=d，E、F分别为AB、CD的中点，则下列表达中成立的是
=
(a＋b＋c＋d)
=a，
=b，
=c,
=d,E、F分别为AB、CD的中点，则下列表达中成立的是（ ）
=
（a+b+c+d） B.
=
（c+d-a-b）
=
（a+b-c-d） D.
=
（a-b+c-d）