题目内容
 如图,半径为1的圆O与等边三角形ABC夹在两平行直线l1,l2之间,l∥l1与圆相交于F,G两点.与三角形ABC两边交于E,D两点,设弧
如图,半径为1的圆O与等边三角形ABC夹在两平行直线l1,l2之间,l∥l1与圆相交于F,G两点.与三角形ABC两边交于E,D两点,设弧 |
| FmG |
A、 |
B、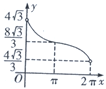 |
C、 |
D、 |
考点:函数的图象
专题:三角函数的图像与性质
分析:根据条件求出圆心角∠FOG=x,利用三角关系求出AP=MR=1-cos
,建立函数关系,即可得到结论.
| x |
| 2 |
解答:解:∵圆的半径为1.∴等边三角形的高为2,即三角形的边长为
∵ 弧
弧
的长为x(0<x<2π),圆的半径为1,
∴圆心角∠FOG=x,
即∠FOR=
,
∴OR=OGcos
=cos
,
∴MR=1-cos
,
又AP=MR=1-cos
,
∴∠PAE=30°
∴cos30°=
,
∴AD=
=
(1-cos
),
∴y=EB+BC+CD=3×
-2AD=4
-
(1-cos
)=
+
cos
,
∴对应的图象为A,
故选:A.
4
| ||
| 3 |
∵
 弧
弧 |
| FmG |
∴圆心角∠FOG=x,
即∠FOR=
| x |
| 2 |
∴OR=OGcos
| x |
| 2 |
| x |
| 2 |
∴MR=1-cos
| x |
| 2 |
又AP=MR=1-cos
| x |
| 2 |
∴∠PAE=30°
∴cos30°=
| AP |
| AD |
∴AD=
| AP |
| cos30° |
| 2 | ||
|
| x |
| 2 |
∴y=EB+BC+CD=3×
4
| ||
| 3 |
| 3 |
| 4 | ||
|
| x |
| 2 |
8
| ||
| 3 |
4
| ||
| 3 |
| x |
| 2 |
∴对应的图象为A,
故选:A.
点评:本题主要考查函数图象的识别和判断,根据条件建立函数关系是解决本题的关键,综合性较强,难度较大.求出RM=AP是解决本题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知集合M={x|x≤1},N={x|0≤x≤2},则M∩N=( )
| A、(-∞,0] | B、[0,1] | C、[1,2] | D、[0,2] |
已知集合U=R,A={x|x≥1或x<0},B={x|x>0},则(∁uA)∩B等于( )
| A、{x|0≤x<1} | B、{x|0<x<1} | C、{x|x≥1} | D、{x|x>0} |
对于函数y=f(x),如果存在区间[m,n],同时满足下列条件:①f(x)在[m,n]是单调的;②当定义域是[m,n]时,f(x)的值域是[2m,2n],则称[m,n]是该函数的“倍值区间”.若函数f(x)=
+a存在“倍值区间”,则a的取值范围是( )
| x+1 |
A、(-
| ||
B、[-
| ||
C、(-
| ||
D、(-
|
函数f(x)=e|x|cosx的部分图象是( )
A、 | B、 | C、 | D、 |
下列函数中,在区间(1,+∞)上是增函数的是( )
| A、y=-x+1 | ||
| B、y=31-x | ||
| C、y=-(x-1)2 | ||
D、y=
|
已知a=lnπ,b=log52,c=e -
,则( )
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、b<c<a |
| D、c<a<b |
设函数g(x)=x2-2(x∈R),f(x)=
,则f(x)的值域是( )
|
A、[-
| ||
| B、[0,+∞) | ||
C、[
| ||
D、[-
|