题目内容
已知数列{an}满足a1=1,an+1=2an+1(n∈N*).
(1)求证:数列{an+1}是等比数列,并写出数列{an}的通项公式;
(2)若数列{bn}满足 ,求
,求 的值.
的值.
证明:(1)an+1=2an+1,
∴an+1+1=2(an+1),
又a1=1,
∴a1+1≠0,an+1≠0,
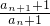 =2,
=2,
∴数列{an+1}是首项为2,公比为2的等比数列.
即an+1=2n,因此an=2n-1. …(6分)
(2)∵ =
= ,
,
∴ =
= ,
,
∴2bn-n=n2,
即bn= (n2+n).…(9分)
(n2+n).…(9分)
∴S=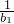 +
+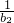 +…+
+…+
=2(1- +
+ -
- +…+
+…+ -
- )
)
=2(1- )
)
= .…(12分)
.…(12分)
分析:(1)根据题意可证得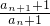 =2,从而可求得an+1的通项公式,继而可得数列{an}的通项公式;
=2,从而可求得an+1的通项公式,继而可得数列{an}的通项公式;
(2)由(1)可知an=2n-1,再由 =
= 可求得bn=
可求得bn= (n2+n),利用裂项法可求得S=
(n2+n),利用裂项法可求得S=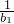 +
+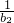 +…+
+…+ 的值.
的值.
点评:本题考查等比数列的通项公式,考查裂项法求和,求得 =2(
=2( -
- )是关键,考查转化与运算能力,属于中档题.
)是关键,考查转化与运算能力,属于中档题.
∴an+1+1=2(an+1),
又a1=1,
∴a1+1≠0,an+1≠0,
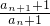 =2,
=2,∴数列{an+1}是首项为2,公比为2的等比数列.
即an+1=2n,因此an=2n-1. …(6分)
(2)∵
 =
= ,
,∴
 =
= ,
,∴2bn-n=n2,
即bn=
 (n2+n).…(9分)
(n2+n).…(9分)∴S=
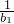 +
+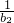 +…+
+…+
=2(1-
 +
+ -
- +…+
+…+ -
- )
)=2(1-
 )
)=
 .…(12分)
.…(12分)分析:(1)根据题意可证得
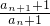 =2,从而可求得an+1的通项公式,继而可得数列{an}的通项公式;
=2,从而可求得an+1的通项公式,继而可得数列{an}的通项公式;(2)由(1)可知an=2n-1,再由
 =
= 可求得bn=
可求得bn= (n2+n),利用裂项法可求得S=
(n2+n),利用裂项法可求得S=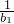 +
+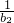 +…+
+…+ 的值.
的值.点评:本题考查等比数列的通项公式,考查裂项法求和,求得
 =2(
=2( -
- )是关键,考查转化与运算能力,属于中档题.
)是关键,考查转化与运算能力,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目