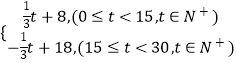题目内容
【题目】(本小题满分12分)
已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,过原点分别作曲线
时,过原点分别作曲线![]() 与
与![]() 的切线
的切线![]() ,
, ![]() ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明: ![]() ;
;
(3)设![]() ,当
,当![]() ,
, ![]() 时,求实数
时,求实数![]() 的取值范围
的取值范围
【答案】(1)单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】(1)求原函数的导函数,对![]() 分类讨论可得原函数的单调区间;(2)背景为指数函数
分类讨论可得原函数的单调区间;(2)背景为指数函数![]() 与对数函数
与对数函数![]() 关于直线
关于直线![]() 对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在性定理的应该用求参数的问题,得到不等式的证明;(3)考查利用导数处理函数的最值和不等式的恒成立求参数的范围问题,求导过程中用到了课后习题
对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在性定理的应该用求参数的问题,得到不等式的证明;(3)考查利用导数处理函数的最值和不等式的恒成立求参数的范围问题,求导过程中用到了课后习题![]() 这个结论,考查学生对知识的掌握程度.
这个结论,考查学生对知识的掌握程度.
(1)依题意,函数![]() 的定义域为
的定义域为![]() ,对
,对![]() 求导,得
求导,得![]() .
.
①若![]() ,对一切
,对一切![]() 有
有![]() ,函数
,函数![]() 的单调递增区间是
的单调递增区间是![]() .
.
②若![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)设切线![]() 的方程为
的方程为![]() ,切点为
,切点为![]() ,则
,则![]() ,
,
![]() ,所以
,所以![]() ,
, ![]() ,则
,则![]() .
.
由题意知,切线![]() 的斜率为
的斜率为![]() ,
, ![]() 的方程为
的方程为![]() .
.
设![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,则
,则![]() ,
,
所以![]() ,
, ![]() .
.
又因为![]() ,消去
,消去![]() 和
和![]() 后,整理得
后,整理得![]() .
.
令![]() ,则
,则![]() ,
, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
若![]() ,
, ![]() ,所以
,所以![]() ,
,
而![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() .
.
若![]() ,因为
,因为![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,则
,则![]() ,
,
所以![]() (舍去).
(舍去).
综上可知, ![]() .
.
(3)![]() ,
, ![]() .
.
①当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
,
![]() 在
在![]() 上递增,
上递增, ![]() 恒成立,符合题意.
恒成立,符合题意.
②当![]() 时,因为
时,因为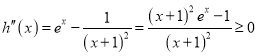 ,所以
,所以![]() 在
在![]() 上递增,且
上递增,且![]() ,则存在
,则存在![]() ,使得
,使得![]() .
.
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,又
上递增,又![]() ,所以
,所以![]() 不恒成立,不合题意.
不恒成立,不合题意.
综合①②可知,所求实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目