题目内容
（本小题满分12分）
已知定点
及椭圆
,过点
的动直线与椭圆相交于
两点．
（1）若线段
中点的横坐标是
，求直线的方程；
（2）在
轴上是否存在点
，使
为常数？若存在，求出点的坐标；若不存在，请说明理由．
解：
（1）依题意，直线
的斜率存在，设直线的方程为
,
将代入
,
消去
整理得
， ………………… 2 分
设
,
|
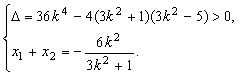
由线段中点的横坐标是
，
得
，解得
，适合①
所以直线的方程为
或
； ……………… 5分
（2）假设在
轴上存在点
，使
为常数．
（ⅰ）当直线与轴不垂直时，由（1）知
， ③
所以
； …………………………7分
将③代入，整理得
，
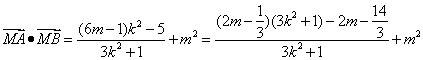
注意到
是与
无关的常数，从而有
，
此时
； ……………………………………………… 10分
（ⅱ）当直线与轴垂直时，此时点
的坐标分别为
，
当
时，亦有 ；
综上，在轴上存在定点
，使为常数. …………… 12分
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
