题目内容
已知函数g(x)=ax3+bx2+cx+d(a≠0)的导函数为f(x),若a+b+c=0,f(0)f(1)>0,设x1,x2是方程f(x)=0的两个根,则|x1-x2|的取值范围为
- A.
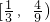
- B.
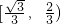
- C.

- D.

B
分析:由题意得:f(x)=3ax2+2bx+c,由x1,x2是方程f(x)=0的两个根,知 .由a+b+c=0,知c=-a-b.由此能求出|x1-x2|的取值范围.
.由a+b+c=0,知c=-a-b.由此能求出|x1-x2|的取值范围.
解答:由题意得:f(x)=3ax2+2bx+c,
∵x1,x2是方程f(x)=0的两个根,
∴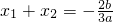 ,
, ,
,
∴|x1-x2|2=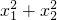 -2x1x2
-2x1x2
=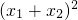 -4x1x2
-4x1x2
=
=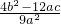 ,
,
∵a+b+c=0,∴c=-a-b,
∴ .
.
∵f(0)•f(1)>0,f(0)=c=-(a+b),f(1)=3a+2b+c=2a+b,
∴(a+b)(2a+b)<0,
即2a2+3ab+b2<0,
∵a≠0,两边同除以a2得: ,
,
所以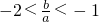 ,故
,故 .
.
故选B.
点评:本题考查根与系数的关系的灵活运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:由题意得:f(x)=3ax2+2bx+c,由x1,x2是方程f(x)=0的两个根,知
 .由a+b+c=0,知c=-a-b.由此能求出|x1-x2|的取值范围.
.由a+b+c=0,知c=-a-b.由此能求出|x1-x2|的取值范围.解答:由题意得:f(x)=3ax2+2bx+c,
∵x1,x2是方程f(x)=0的两个根,
∴
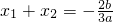 ,
, ,
,∴|x1-x2|2=
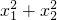 -2x1x2
-2x1x2=
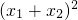 -4x1x2
-4x1x2=

=
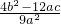 ,
,∵a+b+c=0,∴c=-a-b,
∴
 .
.∵f(0)•f(1)>0,f(0)=c=-(a+b),f(1)=3a+2b+c=2a+b,
∴(a+b)(2a+b)<0,
即2a2+3ab+b2<0,
∵a≠0,两边同除以a2得:
 ,
,所以
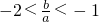 ,故
,故 .
.故选B.
点评:本题考查根与系数的关系的灵活运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目