题目内容
已知函数g(x)=
sin(2x+
),f(x)=acos2(x+
)+b,且函数y=f(x)的图象是函数y=g(x)的图象按向量a=(-
,
)平移得到的.
(1)求实数a、b的值;
(2)设h(x)=g(x)-
f(x),求h(x)的最小值及相应的x的值.
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 4 |
| 1 |
| 2 |
(1)求实数a、b的值;
(2)设h(x)=g(x)-
| 3 |
(1)∵f(x)=acos2(x+
)+b=
cos(2x+
)+
+b,①
g(x)=
sin(2x+
)的图象按向量a=(-
,
)平移得到
f(x)=
sin[2(x+
)+
]+
=
cos(2x+
)+
,②
比较①②可得:a=1,b=0;
(2)∵h(x)=g(x)-
f(x)=
sin(2x+
)-
cos(2x+
)-
=sin(2x+
)-
.
当2x+
=2kπ-
,即x=kπ-
(k∈Z)时,h(x)有最小值,h(x)min=-
.
| π |
| 3 |
| a |
| 2 |
| 2π |
| 3 |
| a |
| 2 |
g(x)=
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 4 |
| 1 |
| 2 |
f(x)=
| 1 |
| 2 |
| π |
| 4 |
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
比较①②可得:a=1,b=0;
(2)∵h(x)=g(x)-
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| ||
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
=sin(2x+
| π |
| 3 |
| 1 |
| 2 |
当2x+
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| 3 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则f(0)= .
,则f(0)= .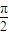 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<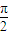 )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )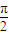 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<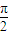 )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )