题目内容
(2012•顺河区一模)向量a=(2,o),b=(x,y),若b与b一a的夹角等于
,则|b|的最大值为
| π | 6 |
4
4
.分析:在平面直角坐标系中,标出
与
对应的点,构造出三角形后运用余弦定理得关于向量|
-
|的方程,由判别式大于等于0可得|b|的最大值.
| a |
| b |
| b |
| a |
解答: 解:如图,设
解:如图,设
=
=(2,0),
=
=(x,y),则
-
=
,
与
-
的夹角为
,即∠OBA=60°,
再设|
|=a,|
|=x,在△OAB中,根据余弦定理有:
22=a2+x2-2×ax×cos
,整理得:x2-
ax+a2-4=0,
由(-
a)2-4(a2-4)≥0,得:a2≤16,所以0<a≤4.
所以|b|的最大值为4.
故答案为4.
 解:如图,设
解:如图,设| OA |
| a |
| OB |
| b |
| b |
| a |
| AB |
| b |
| b |
| a |
| π |
| 6 |
再设|
| OB |
| AB |
22=a2+x2-2×ax×cos
| π |
| 6 |
| 3 |
由(-
| 3 |
所以|b|的最大值为4.
故答案为4.
点评:本题考查了数量积表示两个向量的夹角,考查了方程思想,考查了数形结合思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
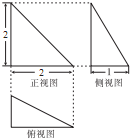 (2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )
(2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )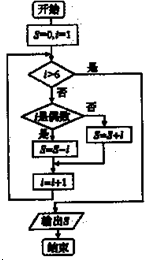 (2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )
(2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )