题目内容
设椭圆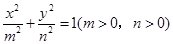 的右焦点与抛物线
的右焦点与抛物线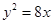 的焦点相同,离心率为
的焦点相同,离心率为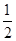 ,则此椭圆的方程为( )
,则此椭圆的方程为( )
A. B.
B.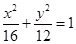
C.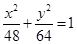 D.
D.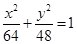
【答案】
B
【解析】
试题分析:因为抛物线的焦点为F(2,0),所以c=2,再由离心率为 ,所以m=4,所以
,所以m=4,所以 所以
所以 .
.
考点:椭圆与抛物线的标准方程,及性质.
点评:由抛物线的焦点,可得椭圆的半焦距c,再由离心率可知m,从而 ,因而椭圆方程确定.
,因而椭圆方程确定.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
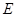 :
: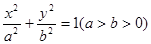 的右焦点
的右焦点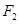 与抛物线
与抛物线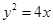 的焦点重合,过
的焦点重合,过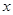 轴垂直的直线
轴垂直的直线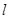 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且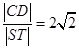 .
.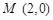 的直线与椭圆
的直线与椭圆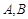 ,设
,设 为椭圆
为椭圆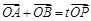 (
(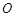 为坐标原点),当
为坐标原点),当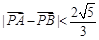 时,求实数
时,求实数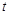 的取值范围.
的取值范围.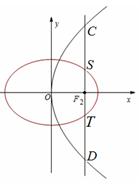
 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,
的焦点相同, ,则此椭圆的方程为_▲__
,则此椭圆的方程为_▲__  的右焦点与抛物线
的右焦点与抛物线 的焦点相同,离心率为
的焦点相同,离心率为 ,则此椭圆的方程为
,则此椭圆的方程为  B.
B. C.
C. D.
D.
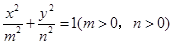 的右焦点与抛物线
的右焦点与抛物线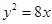 的焦点相同,离心率为
的焦点相同,离心率为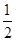 ,则此椭圆的方程为(
)
,则此椭圆的方程为(
)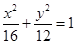 B.
B.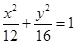 C.
C.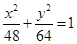 D.
D.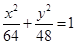
 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,离心率为
的焦点相同,离心率为 ,则此椭圆的方程为( )
,则此椭圆的方程为( ) B.
B. C.
C. D.
D.