题目内容
数列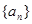 的前
的前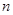 项和记为
项和记为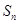 ,
,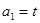 ,
,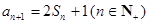 .
.
(I)当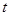 为何值时,数列
为何值时,数列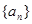 是等比数列?
是等比数列?
(II)在(I)的条件下,若等差数列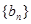 的前
的前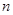 项和
项和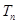 有最大值,且
有最大值,且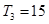 ,又
,又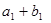 ,
,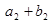 ,
,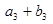 成等比数列,求
成等比数列,求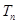 .
.
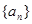 的前
的前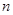 项和记为
项和记为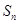 ,
,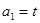 ,
,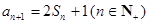 .
.(I)当
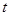 为何值时,数列
为何值时,数列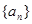 是等比数列?
是等比数列?(II)在(I)的条件下,若等差数列
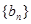 的前
的前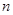 项和
项和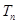 有最大值,且
有最大值,且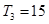 ,又
,又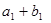 ,
,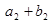 ,
,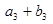 成等比数列,求
成等比数列,求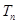 .
.(I)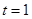 .(II)
.(II)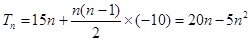 .
.
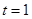 .(II)
.(II)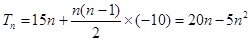 .
.本试题主要是考查了等比数列的定义以及等差数列的前n项和的最值问题的综合运用。
(1)由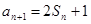 ,可得
,可得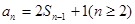 ,
,
两式相减得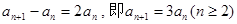 得到数列是等比数列,得到通项公式。
得到数列是等比数列,得到通项公式。
(2)设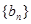 的公差为d,由
的公差为d,由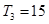 得
得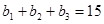 ,于是
,于是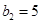 ,
,
故可设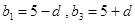 ,又
,又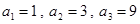 ,得到由题意可得
,得到由题意可得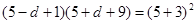 ,解得
,解得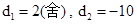 ,进而分析得到结论。
,进而分析得到结论。
解:(I)由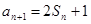 ,可得
,可得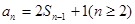 ,
,
两式相减得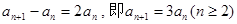 ,
,
∴当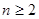 时,
时,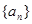 是等比数列,
是等比数列,
要使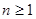 时,
时,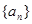 是等比数列,则只需
是等比数列,则只需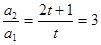 ,从而
,从而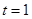 .
.
(II)设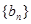 的公差为d,由
的公差为d,由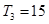 得
得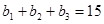 ,于是
,于是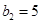 ,
,
故可设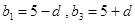 ,又
,又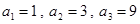 ,
,
由题意可得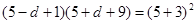 ,解得
,解得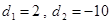 ,
,
∵等差数列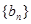 的前
的前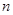 项和
项和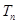 有最大值,∴
有最大值,∴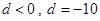
∴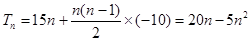 .
.
(1)由
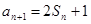 ,可得
,可得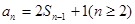 ,
,两式相减得
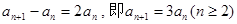 得到数列是等比数列,得到通项公式。
得到数列是等比数列,得到通项公式。(2)设
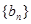 的公差为d,由
的公差为d,由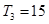 得
得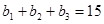 ,于是
,于是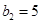 ,
, 故可设
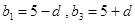 ,又
,又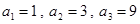 ,得到由题意可得
,得到由题意可得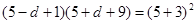 ,解得
,解得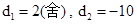 ,进而分析得到结论。
,进而分析得到结论。解:(I)由
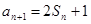 ,可得
,可得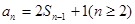 ,
,两式相减得
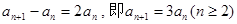 ,
,∴当
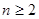 时,
时,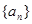 是等比数列,
是等比数列, 要使
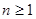 时,
时,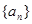 是等比数列,则只需
是等比数列,则只需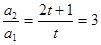 ,从而
,从而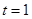 .
. (II)设
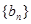 的公差为d,由
的公差为d,由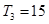 得
得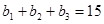 ,于是
,于是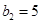 ,
, 故可设
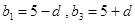 ,又
,又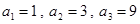 ,
,由题意可得
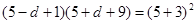 ,解得
,解得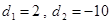 ,
,∵等差数列
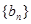 的前
的前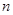 项和
项和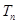 有最大值,∴
有最大值,∴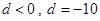
∴
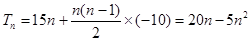 .
.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
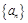 中,若
中,若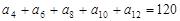 ,则
,则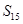 的值为: ( )
的值为: ( )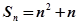 ,那么它的通项公式为an="_________" .
,那么它的通项公式为an="_________" .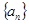 中,
中,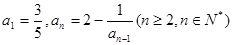 ,数列
,数列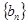 满足
满足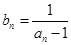 .
.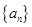 的首项
的首项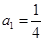 的等比数列,其前
的等比数列,其前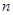 项和
项和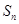 中
中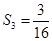 ,
,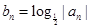 ,
,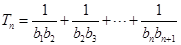 ,求证:
,求证: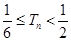
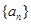 中,
中, 的前n项和,
的前n项和,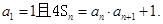
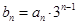 ,数列
,数列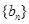 的前n项和为
的前n项和为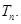 求
求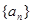 的公差为2,若
的公差为2,若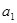 ,
,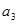 ,
,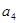 成等比数列,则
成等比数列,则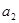 等于( )
等于( )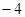 B
B  C
C  D
D 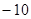
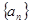 中,
中,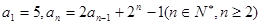 ,若存在实数
,若存在实数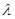 ,使得数列
,使得数列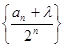 为等差数列,则
为等差数列,则