题目内容
已知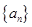 为等差数列,且
为等差数列,且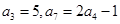 .
.
(Ⅰ)求数列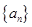 的通项公式及其前
的通项公式及其前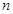 项和
项和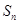 ;
;
(Ⅱ)若数列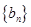 满足
满足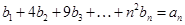 求数列
求数列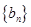 的通项公式.
的通项公式.
【答案】
(Ⅰ) 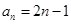 ,
,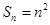 ;(Ⅱ)
;(Ⅱ) 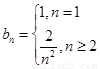 .
.
【解析】
试题分析:(Ⅰ)先设出等差数列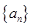 的首项和公差,然后代入式子:
的首项和公差,然后代入式子: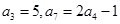 ,列方程组求出首项和公差,再根据等差数列的通项公式:
,列方程组求出首项和公差,再根据等差数列的通项公式: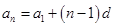 以及前
以及前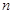 项和公式:
项和公式: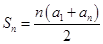 求解;(Ⅱ)由式子
求解;(Ⅱ)由式子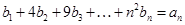 ,取
,取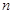 为
为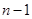 得到:
得到: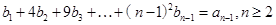 ,两式相减得,
,两式相减得,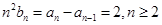 ,结合(Ⅰ)的结果化简整理得,
,结合(Ⅰ)的结果化简整理得,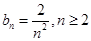 ①,然后求出
①,然后求出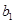 的值,代入①验证,要是不符合那么就把通项写成分段函数的形式,要是符合就合二为一写成一个式子.
的值,代入①验证,要是不符合那么就把通项写成分段函数的形式,要是符合就合二为一写成一个式子.
试题解析:(Ⅰ)设等差数列的首项和公差分别为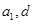 ,
,
则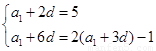 ,解得
,解得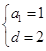 .
2分
.
2分
∴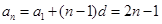 ,
4分
,
4分
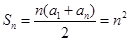 6分
6分
(Ⅱ)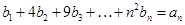 ①,
①,
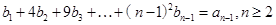 ②,
7分
②,
7分
① ②得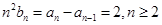 ,
8分
,
8分
∴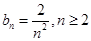 ,
10分
,
10分
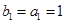 ,
11分
,
11分
∴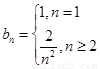 .
12分
.
12分
考点:1.等差数列的通项公式;2.等差数列的前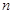 项和;3.数列的递推公式
项和;3.数列的递推公式

练习册系列答案
相关题目
 为等差数列,且
为等差数列,且 .
. 项和
项和 ;
; 满足
满足 求数列
求数列 为等差数列,且
为等差数列,且 ,
, .
. 项和
项和 的最小值;
的最小值; 满足
满足 ,
, ,求
,求 .
.
 为等差数列,且
为等差数列,且 (Ⅰ)求数列
(Ⅰ)求数列 项和为
项和为 ,若
,若 成等比数列,求正整数
成等比数列,求正整数 的值。
的值。 为等差数列,且
为等差数列,且 ,
, 。(Ⅰ)求
。(Ⅰ)求 满足
满足 ,
, ,求
,求 为等差数列,且
为等差数列,且 ,
, 。
。 满足
满足 ,
, ,求
,求