题目内容
在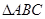 中,
中,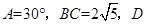 是
是 边上的一点,
边上的一点,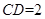 ,
, 的面积是4,则AC长为 .
的面积是4,则AC长为 .
 或4
或4
解析试题分析:因为, ,所以,
,所以, ,
, ,
, ,
,
因在△BDC中:BD²=CD²+BC²-2CB×CD×cos∠DCB  或
或  ,
,
即BD=4;或BD=4 。
。
由正弦定理得,
故,  ,即:
,即: 或
或  。
。
在△ABC中
即:
解得,AC的长为 或4。
或4。
考点:本题主要考查正弦定理、余弦定理的应用,三角形面积公式。
点评:中档题,本题综合考查正弦定理、余弦定理的应用,三角形面积公式。解答过程看似复杂,应注意结合三角形认真分析,防止漏解。本题易错。

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 中,
中, 面积
面积 ,则
,则 等于 。
等于 。 ,则这个三角形的面积是 。
,则这个三角形的面积是 。 ,
,
 中,
中, ,那么A=_____________;
,那么A=_____________; 中,
中, 所对的边分别是
所对的边分别是 ,已知
,已知 ,则
,则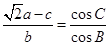 ,则B的大小为 .
,则B的大小为 .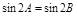 ,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若
,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若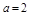 ,
,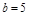 ,
,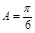 ,则△ABC有两组解;③设
,则△ABC有两组解;③设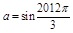 ,
,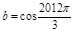 ,
,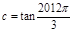 ,则
,则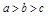 ;④将函数
;④将函数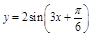 图象向左平移
图象向左平移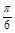 个单位,得到函数
个单位,得到函数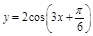 图象。其中正确命题的个数是 .
图象。其中正确命题的个数是 .  ,b=12,
,b=12, ,则
,则 的值为__________.
的值为__________.