Question

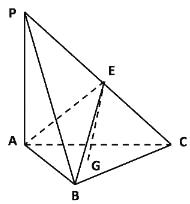
【题目】如图，在三棱锥P﹣ABC中，平面PAC⊥平面ABC，PA⊥AC，AB=BC=CA=AP=2，G是△ABC重心，E是线段PC上一点，且CE=λCP．

（1）当EG∥平面PAB时，求λ的值；

（2）当直线CP与平面ABE所成角的正弦值为时，求λ的值．

Answer 1

【答案】（1）；（2）或.

【解析】

（1）取AB的中点D，连结PD，CD，根据线面平行的性质可得EG∥PD，从而得出λ的值；

（2）建立空间坐标系，求出平面ABE的法向量，根据夹角公式得出λ的值．

（1）取AB的中点D，连结PD，CD，

∵AB=BC=AC，G是△ABC重心，

∴G是CD的三等分点，且CG=CD，

∵EG∥平面PAB，EG平面PCD，平面PCD∩平面PAB=PD，

∴EG∥PD，

∴，即λ=．

（2）以A为坐标原点，以AC，AP为y轴，z轴作空间直角坐标系

A﹣xyz，如图所示：

则A（0，0，0），B（，1，0），C（0，2，0），

P（0，0，2），E（0，2﹣2λ，2λ），

∴=（0，﹣2，2），=（，1，0），=（0，2﹣2λ，2λ），

设平面ABE的法向量为=（x，y，z），则， =0，

∴，令x=1可得，y=﹣，z=．

∴=（1，﹣，），

∴cos＜，＞===，

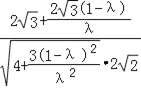∴当直线CP与平面ABE所成角的正弦值为时， =，

∴2=，即28λ2﹣24λ+5=0．

解得λ=或λ=．