题目内容
已知递增等比数列{bn}满足b2•b4=64,b5=32,数列{an}满足an-bn=
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列cn=nan,求数列{cn}的前n项和Tn.
| 1 |
| 2n |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列cn=nan,求数列{cn}的前n项和Tn.
(Ⅰ)∵递增等比数列{bn}满足b2•b4=64,b5=32,设公比为q,则有 b12 q5=64,且 b1q4=32,
解得 b1=2,q=2,bn=2n.
再由 {an}满足an-bn=
,可得 an=bn+
=2n+
.
(Ⅱ)∵数列cn=nan,∴cn =n 2n+
.
∴数列{cn}的前n项和Tn=1×2+2×22+3×23+…+n•2n+
令 s=1×2+2×22+3×23+…+n•2n ①,则 2s=1×22+2×23+3×24+…+n•2n+1 ②.
①-②可得-s=2+22+23+…+2n-n•2n+1=2n+1-2-n•2n+1,
∴s=(n-1)2n+1+2,∴Tn=s+
=(n-1)2n+1+2+
.
解得 b1=2,q=2,bn=2n.
再由 {an}满足an-bn=
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
(Ⅱ)∵数列cn=nan,∴cn =n 2n+
| 1 |
| 2 |
∴数列{cn}的前n项和Tn=1×2+2×22+3×23+…+n•2n+
| n |
| 2 |
令 s=1×2+2×22+3×23+…+n•2n ①,则 2s=1×22+2×23+3×24+…+n•2n+1 ②.
①-②可得-s=2+22+23+…+2n-n•2n+1=2n+1-2-n•2n+1,
∴s=(n-1)2n+1+2,∴Tn=s+
| n |
| 2 |
| n |
| 2 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目


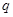 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与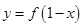 图像关于
图像关于 对称.
对称. 满足
满足 和
和 ,则
,则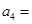
 D、8或
D、8或