题目内容

已知A、B、C三点不共线，点O为平面ABC外的一点，则下列条件中，能得 到平面ABC的充分条件是  （    ）

A．；         B．；

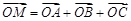C．；            D．

 

【答案】

A

【解析】

试题分析：A．,因为，所以四点A、B、C、O共面；

B．，因为，所以四点A、B、C、O不共面；

C．，因为，所以四点A、B、C、O不共面；

D．，因为，所以四点A、B、C、O不共面。

考点:向量共线的条件；向量共面的条件。

点评：本题给出关于向量的几个线性表达式，叫我们判断能使点M∈平面ABC的充分条件，着重考查了利用空间向量判断四点共面的方法，属于基础题．

 

练习册系列答案
相关题目
已知A、B、C三点不共线，且点O满足
OA
+
OB
+
OC
=0，则下列结论正确的是（　　）
A、
OA
=
1
3
AB
+
2
3
BC
B、
OA
=
2
3
AB
+
1
3
BC
C、
OA
=-
1
3
AB
-
2
3
BC
D、
OA
=-
2
3
AB
-
1
3
BC
已知A、B、C三点不共线，O是平面ABC外的任一点，下列条件中能确定点M与点A、B、C一定共面的是（　　）
A、
OM
=
OA
+
OB
+
OC
B、
OM
=2
OA
-
OB
-
OC
C、
OM
=
OA
+
1
2
OB
+
1
3
OC
D、
OM
=
1
3
OA
+
1
3
OB
+
1
3
OC
已知A、B、C三点不共线，M、A、B、C四点共面，则对平面ABC外的任一点O，有
OM
=
1
2
OA
+
1
3
OB
+t
OC
，则t=
 
．
已知A，B，C三点不共线，对平面ABC外一点O，给出下列命题：
①
OM
=
1
3
OA
+
1
3
OB
+
1
3
OC
；       ②
OM
=
OA
-
OB
+
OC
；
③
OM
=
OA
+2
OB
+
AC
；          ④
OM
=2
OA
+
OB
+
AC
．
其中，能推出M，A，B，C四点共面的是（　　）
已知A，B，C三点不共线，点O是平面ABC外一点，则在下列条件中，能得到点M与A，B，C一定共面的一个条件为
④
④
． （填序号）
①
OM
=
1
2
OA
+
1
2
OB
+
1
2
OC
；②
OM
=2
OA
-
OB
-
OC
；
③
OM
=
OA
+
OB
+
OC
；④
OM
=
1
3
OA
-
1
3
OB
+
OC
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网