题目内容
(本小题满分8分)对于函数 ,若存在实数
,若存在实数 ,使
,使 =
= 成立,则称
成立,则称 为
为 的不动点.
的不动点.
⑴当 时,求
时,求 的不动点;
的不动点;
⑵若对于任意实数 ,函数
,函数 恒有两个不相同的不动点,求
恒有两个不相同的不动点,求 的取值范围.
的取值范围.
 ,若存在实数
,若存在实数 ,使
,使 =
= 成立,则称
成立,则称 为
为 的不动点.
的不动点.⑴当
 时,求
时,求 的不动点;
的不动点;⑵若对于任意实数
 ,函数
,函数 恒有两个不相同的不动点,求
恒有两个不相同的不动点,求 的取值范围.
的取值范围.⑴ 的不动点为-1和2.⑵
的不动点为-1和2.⑵
 的不动点为-1和2.⑵
的不动点为-1和2.⑵
解:⑴由题义
整理得 ,解方程得
,解方程得
即 的不动点为-1和2. ………………………3分
的不动点为-1和2. ………………………3分
⑵由 =
= 得
得
如此方程有两解,则有△=
把 看作是关于
看作是关于 的二次函数,则有
的二次函数,则有

解得 即为所求. ………………………8分
即为所求. ………………………8分

整理得
 ,解方程得
,解方程得
即
 的不动点为-1和2. ………………………3分
的不动点为-1和2. ………………………3分⑵由
 =
= 得
得
如此方程有两解,则有△=

把
 看作是关于
看作是关于 的二次函数,则有
的二次函数,则有
解得
 即为所求. ………………………8分
即为所求. ………………………8分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示: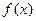 关于时间
关于时间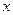 的函数表达式(
的函数表达式(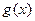 与时间
与时间 :
: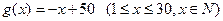 ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?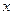 (元),年销售量为
(元),年销售量为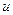 (万件),平均每件纪念品的利润为
(万件),平均每件纪念品的利润为 (元).
(元).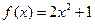 ,值域为
,值域为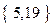 的“孪生函数”共有_______个.
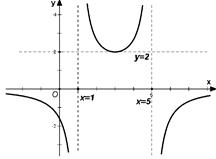
的“孪生函数”共有_______个. ,其图象如图所示,
,其图象如图所示,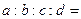 .
.
 的图象向左平移2个单位,再向上平移1个单位后
的图象向左平移2个单位,再向上平移1个单位后 的图象是以原点为圆心,1为半径的两段圆弧,则不等式
的图象是以原点为圆心,1为半径的两段圆弧,则不等式 的解集为 ( )
的解集为 ( )



