题目内容
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
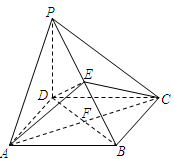
(1)求证:AC⊥DE;
(2)求四棱锥P-ABCD的体积.

(1)求证:AC⊥DE;
(2)求四棱锥P-ABCD的体积.
(1)详见解析,(2) .
.
 .
.试题分析:(1)证明线线垂直,一般利用线面垂直性质与判定定理进行转化. 因为四边形ABCD是菱形,所以AC⊥BD.又因为PD⊥平面ABCD,所以PD⊥AC.因而AC⊥平面PDB,从而AC⊥DE.(2)设AC与BD相交于点F.连EF.由(1),知AC⊥平面PDB,所以AC⊥EF.所以S△ACE=
 AC·EF,因此△ACE面积最小时,EF最小,则EF⊥PB.由△PDB∽△FEB,解得PD=
AC·EF,因此△ACE面积最小时,EF最小,则EF⊥PB.由△PDB∽△FEB,解得PD= ,因为PD⊥平面ABCD,所以VP—ABCD=
,因为PD⊥平面ABCD,所以VP—ABCD= S□ABCD·PD=
S□ABCD·PD= ×24×
×24× =
= .
.(1)证明:连接BD,设AC与BD相交于点F.
因为四边形ABCD是菱形,所以AC⊥BD.
又因为PD⊥平面ABCD,AC
 平面ABCD,所以PD⊥AC.
平面ABCD,所以PD⊥AC.而AC∩BD=F,所以AC⊥平面PDB.
E为PB上任意一点,DE
 平面PBD,所以AC⊥DE.
平面PBD,所以AC⊥DE.(2)连EF.由(1),知AC⊥平面PDB,EF
 平面PBD,所以AC⊥EF. S△ACE=
平面PBD,所以AC⊥EF. S△ACE= AC·EF,在△ACE面积最小时,EF最小,则EF⊥PB.
AC·EF,在△ACE面积最小时,EF最小,则EF⊥PB. S△ACE=3,
 ×6×EF=3,解得EF=1.
×6×EF=3,解得EF=1. 由△PDB∽△FEB,得
 .由于EF=1,FB=4,
.由于EF=1,FB=4, ,
,所以PB=4PD,即
 .解得PD=
.解得PD=
VP—ABCD=
 S□ABCD·PD=
S□ABCD·PD= ×24×
×24× =
= .
.
练习册系列答案
相关题目
 为矩形,
为矩形, 平面
平面 ,
, ,作如图3折叠,折痕
,作如图3折叠,折痕 .其中点
.其中点 、
、 分别在线段
分别在线段 、
、 上,沿
上,沿 折叠后点
折叠后点 在线段
在线段 上的点记为
上的点记为 ,并且
,并且 .
.
 平面
平面 ;
; 的体积.
的体积.
 中,
中, 底面
底面 ,
,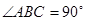 ,且
,且 ,
, 是
是 的中点,
的中点, 且交
且交 于点
于点 .
. 平面
平面 ;
; 时,求三棱锥
时,求三棱锥 的体积.
的体积.
 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高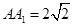 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点. 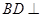 平面
平面 ;
; ∥平面
∥平面 ;
; 的体积.
的体积.
 的边长为3,
的边长为3, 与
与 交于
交于 ,且
,且 .将菱形
.将菱形 折起得到三棱锥
折起得到三棱锥 (如图),点
(如图),点 是棱
是棱 的中点,
的中点, .
.
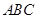
 平面
平面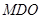 ;
; 的体积.
的体积. ,那么正方体的棱长等于( )
,那么正方体的棱长等于( )



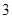 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )


