题目内容
从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x﹣y|≤5的事件概率.
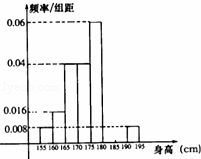
解:(1)由频率分布直方图知,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,
后三组频率为1﹣0.82=0.18,人数为0.18×50=9人(2分)
这所学校高三男生身高在180cm以上(含180cm)的人数为800×0.18=144人(4分)
(2)由频率分布直方图得第八组频率为0.008×5=0.04,人数为0.04×50=2人,
设第六组人数为m,则第七组人数为9﹣2﹣m=7﹣m,又m+2=2(7﹣m),所以m=4,
即第六组人数为4人,第七组人数为3人,频率分别为0.08,0.06,(6分)
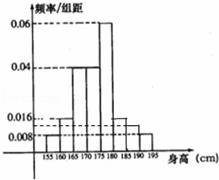
频率除以组距分别等于0.016,0.012,见图(8分)
(3)由(2)知身高在[180,185]内的人数为4人,设为a,b,c,d.身高在[190,195]的人数为2人,设为A,B.
若x,y∈[180,185]时,有ab,ac,ad,bc,bd,cd共六种情况.
若x,y∈[190,195]时,有AB共一种情况.
若x,y分别在[180,185],[190,195]内时,有aA,bA,cA,dA,aB,bB,cB,dB共8种情况
所以基本事件的总数为6+8+1=15种(12分)
事件|x﹣y|≤5所包含的基本事件个数有6+1=7种,故![]() (14分)
(14分)

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案