题目内容
已知双曲线![]() (a>0,b>0)的两条渐近线互相垂直,F(2,0)是它的一个焦点.
(a>0,b>0)的两条渐近线互相垂直,F(2,0)是它的一个焦点.
(1)求双曲线的方程;
(2)过点F作互相垂直的两条直线l1、l2,l1交双曲线于A、B两点,l2交双曲线于C、D两点,
求![]() 的值.
的值.
20.解:(1)∵ 双曲线的渐近线方程为![]() ,∴
,∴ ![]() ,
,
得 a2 = b2,于是 c2 = a2 + b2 = 2a2 = 4,因此 a2 = 2,b2 = 2.所以双曲线的方程为![]() . 4分
. 4分
(2)① 当直线l1、l2其中一条与x轴垂直,不妨设l1⊥x轴时,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴ ![]() ,
,![]() ,
,
∴ ![]() . … 5分
. … 5分
② 当直线l1、l2都不与x轴垂直时,
设l1:y = k(x-2),k≠0,则 l2:![]() .
.
由 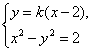 消去y,整理得(k2-1)x2-4k2x + 4k2 + 2 = 0.
消去y,整理得(k2-1)x2-4k2x + 4k2 + 2 = 0.
∵ l1与双曲线有两个交点为A(x1,y1),B(x2,y2),
∴ ![]() ,
,![]() ,且
,且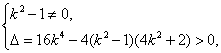 得 k≠±1.
得 k≠±1.
又 y1y2 = k (x1-2) k (x2-2),![]() ,
,![]() ,
,
∴ ![]() (1 + k2 )(x1-2) (x2-2)
(1 + k2 )(x1-2) (x2-2)
= (1 + k2) [ x1x2-2(x1 + x2) + 4 ] =![]() . ………… 8分
. ………… 8分
以![]() 代k得
代k得 ![]() , ∴
, ∴ ![]() .
.
综合①②,得![]() . …………… 12分
. …………… 12分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目











 (a>0,b>0)的左右焦点分别为F1、 F2 ,P 是双曲线上的一点,且P F1⊥P F2,
(a>0,b>0)的左右焦点分别为F1、 F2 ,P 是双曲线上的一点,且P F1⊥P F2,  的面积为2 ab,则双曲线的离心率 e=________.
的面积为2 ab,则双曲线的离心率 e=________. (a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( ) (B)
(B) (C)
(C) (D)
(D)