题目内容
(2013•和平区二模)一个总体可分为A,B,C三层,它们的个体数之比为3:6:1,用分层抽样的方法从总体中抽取-个容量为20的样本,已知C层中甲、乙均被抽到的概率为
,则总体中的个体数是
| 1 | 21 |
70
70
.分析:先求出C层中的个体数占总体数的比例为
,可得从C层中抽取了20×
=2个样本.设C层中的个体数为n,由
=
,解得n的值,可得总体中的个体数.
| 1 |
| 10 |
| 1 |
| 10 |
| ||
|
| 1 |
| 21 |
解答:解:根据分层抽样的定义和方法,C层中的个体数占总体数的比例为
=
,
故从C层个体中抽取的样本数占样本容量的
,故从C层中抽取了20×
=2个样本.
设C层中的个体数为n,由题意可得
=
,解得n=7,故总体中的个体数为 7÷
=70,
故答案为 70.
| 1 |
| 3+6+1 |
| 1 |
| 10 |
故从C层个体中抽取的样本数占样本容量的
| 1 |
| 10 |
| 1 |
| 10 |
设C层中的个体数为n,由题意可得
| ||
|
| 1 |
| 21 |
| 1 |
| 10 |
故答案为 70.
点评:本题主要考查分层抽样的定义和方法,利用了总体中各层的个体数之比等于样本中对应各层的样本数之比,每个个体被抽到的概率都相等,属于基础题.

练习册系列答案
相关题目
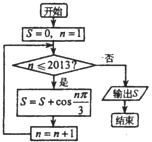 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )