题目内容
定义在(-1,1)上的函数f(x)满足:①对任意 ,②当x∈(-1,0)时,有f(x)>0;若
,②当x∈(-1,0)时,有f(x)>0;若 ,
, ,R=f(0),则P,Q,R的大小关系为________(用“<”连接)
,R=f(0),则P,Q,R的大小关系为________(用“<”连接)
Q<P<R
分析:对于f(x)-f(y)=f( ),当x<y时,-1<
),当x<y时,-1< <0,同时有xy<1,可得f(x)-f(y)=f(
<0,同时有xy<1,可得f(x)-f(y)=f( )>0,即f(x)-f(y)>0,可得f(x)为减函数,进而分析P可得,P=f(
)>0,即f(x)-f(y)>0,可得f(x)为减函数,进而分析P可得,P=f( )-f(
)-f( )+f(
)+f( )-f(
)-f( )+…+f(
)+…+f(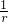 )-f(
)-f( )+…+f(
)+…+f( )-f(
)-f( ),消项可得p=f(
),消项可得p=f( )-f(
)-f( )=f(
)=f( )=f(
)=f( ),结合函数的单调性,可得答案.
),结合函数的单调性,可得答案.
解答:根据题意,若x、y∈(-1,1),有(1-xy)2-(x-y)2=(1-x2)(1-y2)>0,即(1-xy)2>(x-y)2,
则可得-1< <1,
<1,
当x<y时,易得xy<1,进而可得-1< <0,此时有f(x)-f(y)=f(
<0,此时有f(x)-f(y)=f( )>0,即f(x)-f(y)>0,
)>0,即f(x)-f(y)>0,
则f(x)为减函数,
对于P,f( )=f(
)=f( )=f(
)=f(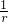 )-f(
)-f( ),
),
则P=f( )-f(
)-f( )+f(
)+f( )-f(
)-f( )+…+f(
)+…+f(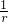 )-f(
)-f( )+…+f(
)+…+f( )-f(
)-f( )=f(
)=f( )-f(
)-f( )=f(
)=f( )=f(
)=f( ),
),
易得0< <
< ,根据f(x)为减函数,
,根据f(x)为减函数,
可得f(0)>f( )>f(
)>f( ),
),
即Q<P<R;
故答案为Q<P<R.
点评:本题考查抽象函数的应用,关键在于根据题意,判断函数的单调性,难点在于对P的转化.
分析:对于f(x)-f(y)=f(
 ),当x<y时,-1<
),当x<y时,-1< <0,同时有xy<1,可得f(x)-f(y)=f(
<0,同时有xy<1,可得f(x)-f(y)=f( )>0,即f(x)-f(y)>0,可得f(x)为减函数,进而分析P可得,P=f(
)>0,即f(x)-f(y)>0,可得f(x)为减函数,进而分析P可得,P=f( )-f(
)-f( )+f(
)+f( )-f(
)-f( )+…+f(
)+…+f(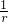 )-f(
)-f( )+…+f(
)+…+f( )-f(
)-f( ),消项可得p=f(
),消项可得p=f( )-f(
)-f( )=f(
)=f( )=f(
)=f( ),结合函数的单调性,可得答案.
),结合函数的单调性,可得答案.解答:根据题意,若x、y∈(-1,1),有(1-xy)2-(x-y)2=(1-x2)(1-y2)>0,即(1-xy)2>(x-y)2,
则可得-1<
 <1,
<1,当x<y时,易得xy<1,进而可得-1<
 <0,此时有f(x)-f(y)=f(
<0,此时有f(x)-f(y)=f( )>0,即f(x)-f(y)>0,
)>0,即f(x)-f(y)>0,则f(x)为减函数,
对于P,f(
 )=f(
)=f( )=f(
)=f(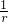 )-f(
)-f( ),
),则P=f(
 )-f(
)-f( )+f(
)+f( )-f(
)-f( )+…+f(
)+…+f(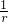 )-f(
)-f( )+…+f(
)+…+f( )-f(
)-f( )=f(
)=f( )-f(
)-f( )=f(
)=f( )=f(
)=f( ),
),易得0<
 <
< ,根据f(x)为减函数,
,根据f(x)为减函数,可得f(0)>f(
 )>f(
)>f( ),
),即Q<P<R;
故答案为Q<P<R.
点评:本题考查抽象函数的应用,关键在于根据题意,判断函数的单调性,难点在于对P的转化.

练习册系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.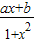 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.