题目内容
已知等差数列{an}的公差d大于0,且a2、a5是方程x2-12x+27=0的两根,数列{bn}的前n项和为Tn,且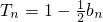 .
.
(1)求数列{an}、{bn}的通项公式;
(2)设数列{an}的前n项和为Sn,试判断n≥4时 与Sn+1的大小,并用数学归纳法证明你的结论.
与Sn+1的大小,并用数学归纳法证明你的结论.
解:(1)设an的首项为a1,∵a2,a5是方程x2-12x+27=0的两根,
∴ ,∴
,∴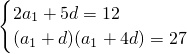
∴a1=1,d=2,∴an=2n-1
n=1时,b1=T1=1- b1,∴b1=
b1,∴b1=
n≥2时,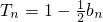 ,
,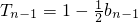 ,
,
两式相减得bn= bn-1数列是等比数列,
bn-1数列是等比数列,
∴bn= •(
•( )n-1;
)n-1;
(2)Sn=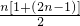 =n2,∴Sn+1=(n+1)2,
=n2,∴Sn+1=(n+1)2, =
=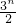
n≥4时, >Sn+1,证明如下:
>Sn+1,证明如下:
下面用数学归纳法证明:①当n=4时,已证.
②假设当n=k (k∈N*,k≥4)时,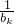 >Sk+1,即
>Sk+1,即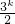 >(k+1)2.
>(k+1)2.
那么n=k+1时,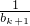 =
=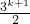 =3•
=3•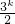 >3(k+1)2=3k2+6k+3
>3(k+1)2=3k2+6k+3
=(k2+4k+4)+2k2+2k-1>[(k+1)+1]2=S(k+1)+1,
∴n=k+1时,结论也成立.
由①②可知n∈N*,n≥4时, >Sn+1都成立.
>Sn+1都成立.
分析:(1)由于数列{an}是等差数列,故只需求出首项和公差就可求其通项公式;由数列{bn}的前n项和为Tn 通过递推然后两式相减可求得bn.
(2)利用等差数列求和公式得出Sn,Sn+1.猜想:n≥4时, >Sn+1,最后利用数学归纳法证明.
>Sn+1,最后利用数学归纳法证明.
点评:本小题主要考查等差数列的通项公式、等比数列的通项公式、数列与不等式的综合、数学归纳法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
∴
 ,∴
,∴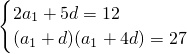
∴a1=1,d=2,∴an=2n-1
n=1时,b1=T1=1-
 b1,∴b1=
b1,∴b1=
n≥2时,
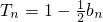 ,
,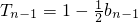 ,
,两式相减得bn=
 bn-1数列是等比数列,
bn-1数列是等比数列,∴bn=
 •(
•( )n-1;
)n-1;(2)Sn=
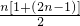 =n2,∴Sn+1=(n+1)2,
=n2,∴Sn+1=(n+1)2, =
=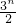
n≥4时,
 >Sn+1,证明如下:
>Sn+1,证明如下:下面用数学归纳法证明:①当n=4时,已证.
②假设当n=k (k∈N*,k≥4)时,
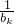 >Sk+1,即
>Sk+1,即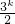 >(k+1)2.
>(k+1)2.那么n=k+1时,
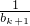 =
=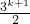 =3•
=3•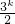 >3(k+1)2=3k2+6k+3
>3(k+1)2=3k2+6k+3=(k2+4k+4)+2k2+2k-1>[(k+1)+1]2=S(k+1)+1,
∴n=k+1时,结论也成立.
由①②可知n∈N*,n≥4时,
 >Sn+1都成立.
>Sn+1都成立.分析:(1)由于数列{an}是等差数列,故只需求出首项和公差就可求其通项公式;由数列{bn}的前n项和为Tn 通过递推然后两式相减可求得bn.
(2)利用等差数列求和公式得出Sn,Sn+1.猜想:n≥4时,
 >Sn+1,最后利用数学归纳法证明.
>Sn+1,最后利用数学归纳法证明.点评:本小题主要考查等差数列的通项公式、等比数列的通项公式、数列与不等式的综合、数学归纳法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.