题目内容
求函数
单调递增区间和值域．
【答案】分析：本题是一个复合函数的单调区间和值域求解问题，由于外函数是一个以
为底的指数函数，故求复合函数的单调递增区间的即求内函数的单调递减区间，根据二次函数的性质，求出内函数的单调递减区间和值域后，即可得到答案．
解答：解：设t（x）=x2-6x+6=（x-3）2-3
则t（x）的单调递减区间为（-∞，3]，值域为[-3，+∞）
∵函数y=
为减函数，
故
的单调递增区间为（-∞，3]，
值域为（0，8]
点评：本题考查的知识点是复合函数的单调性，函数的值域，指数函数的性质及二次函数的性质，其中根据复合函数单调性“同增异减”的法则，将问题转化为求二次函数的单调递减区间问题是解答本题的关键．
为底的指数函数，故求复合函数的单调递增区间的即求内函数的单调递减区间，根据二次函数的性质，求出内函数的单调递减区间和值域后，即可得到答案．解答：解：设t（x）=x2-6x+6=（x-3）2-3
则t（x）的单调递减区间为（-∞，3]，值域为[-3，+∞）
∵函数y=
为减函数，故
的单调递增区间为（-∞，3]，值域为（0，8]
点评：本题考查的知识点是复合函数的单调性，函数的值域，指数函数的性质及二次函数的性质，其中根据复合函数单调性“同增异减”的法则，将问题转化为求二次函数的单调递减区间问题是解答本题的关键．
练习册系列答案
相关题目
的最小正周期和最大值；
单调递增区间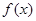
＝
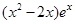（e为自然对数的底数） 
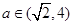,求函数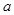
]上的最大值和最小值．（5分）
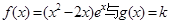的图象有三个不同的交点，求实数k的取值范围.
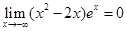)（2分）
单调递增区间和值域．