题目内容
【题目】已知△ABC的两个顶点A,B的坐标分别为(![]() ,0),(
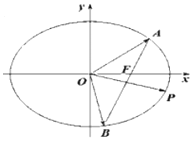
,0),(![]() ,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2
,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2![]() ,动点C的轨迹为曲线G.
,动点C的轨迹为曲线G.
(1)求曲线G的方程;
(2)设直线l与曲线G交于M,N两点,点D在曲线G上,![]() 是坐标原点
是坐标原点![]() ,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
【答案】(1)![]()
![]() .(2)四边形OMDN的面积是定值,其定值为
.(2)四边形OMDN的面积是定值,其定值为![]() .
.
【解析】
(1)根据三角形内切圆的性质证得![]() ,由此判断出
,由此判断出![]() 点的轨迹为椭圆,并由此求得曲线
点的轨迹为椭圆,并由此求得曲线![]() 的方程.
的方程.
(2)将直线![]() 的斜率分成不存在或存在两种情况,求出平行四边形
的斜率分成不存在或存在两种情况,求出平行四边形![]() 的面积,两种情况下四边形
的面积,两种情况下四边形![]() 的面积都为
的面积都为![]() ,由此证得四边形
,由此证得四边形![]() 的面积为定值.
的面积为定值.
(1)因为圆E为△ABC的内切圆,所以|CA|+|CB|=|CP|+|CQ|+|PA|+|QB|=2|CP|+|AR|+|BR|=2|CP|+|AB|=4>|AB|
所以点C的轨迹为以点A和点B为焦点的椭圆(点![]() 不在
不在![]() 轴上),
轴上),
所以c![]() ,a=2,b
,a=2,b![]() ,
,
所以曲线G的方程为![]()
![]() ,
,
(2)因为![]() ,故四边形
,故四边形![]() 为平行四边形.
为平行四边形.
当直线l的斜率不存在时,则四边形![]() 为为菱形,
为为菱形,
故直线MN的方程为x=﹣1或x=1,
此时可求得四边形OMDN的面积为![]() .
.
当直线l的斜率存在时,设直线l方程是y=kx+m,
代入到![]() ,得(1+2k2)x2+4kmx+2m2﹣4=0,
,得(1+2k2)x2+4kmx+2m2﹣4=0,
∴x1+x2![]() ,x1x2
,x1x2![]() ,△=8(4k2+2﹣m2)>0,
,△=8(4k2+2﹣m2)>0,
∴y1+y2=k(x1+x2)+2m![]() ,|MN|
,|MN|![]()
点O到直线MN的距离d ,
,
由![]() ,得xD
,得xD![]() ,yD
,yD![]() ,
,
∵点D在曲线C上,所以将D点坐标代入椭圆方程得1+2k2=2m2,
由题意四边形OMDN为平行四边形,
∴OMDN的面积为S ,
,
由1+2k2=2m2得S![]() ,
,
故四边形OMDN的面积是定值,其定值为![]() .
.

【题目】某啤酒厂要将一批鲜啤酒用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,运费由厂家承担.若厂家恰能在约定日期(×月×日)将啤酒送到,则城市乙的销售商一次性支付给厂家40万元;若在约定日期前送到,每提前一天销售商将多支付给厂家2万;若在约定日期后送到,每迟到一天销售商将少支付给厂家2万元.为保证啤酒新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送.已知下表内的信息:
汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路1 | 1 | 4 |
| 2 |
公路2 | 2 | 3 |
| 1 |
(1)记汽车选择公路1运送啤酒时厂家获得的毛收入为X(单位:万元),求X的分布列和EX;
(2)若![]() ,
,![]() ,选择哪条公路运送啤酒厂家获得的毛收人更多?
,选择哪条公路运送啤酒厂家获得的毛收人更多?
(注:毛收入=销售商支付给厂家的费用-运费).