题目内容
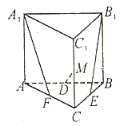
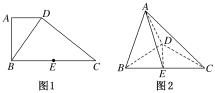
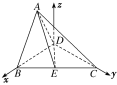
【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
若AD=1,二面角CABD的平面角的正切值为![]() ,求二面角BADE的余弦值.
,求二面角BADE的余弦值.
【答案】![]()
【解析】
根据已知可得![]() 平面
平面![]() ,
,![]() ,进而有AB⊥平面ADC,得出二面角CABD的平面角为∠CAD,求出
,进而有AB⊥平面ADC,得出二面角CABD的平面角为∠CAD,求出![]() ,以D为坐标原点,建立如图所示的空间直角坐标系,确定点
,以D为坐标原点,建立如图所示的空间直角坐标系,确定点![]() 坐标,求出平面BAD的法向量坐标,利用平面BAD的一个法向量
坐标,求出平面BAD的法向量坐标,利用平面BAD的一个法向量![]() =(0,1,0),由空间向量面面角公式,即可求解.
=(0,1,0),由空间向量面面角公式,即可求解.
平面ABD⊥平面BCD,平面ABD![]() 平面BCD
平面BCD![]() ,
,
BD⊥DC,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
AB⊥平面ADC,![]() ,
,
所以二面角CABD的平面角为∠CAD.
又DC⊥平面ABD,AD平面ABD,所以DC⊥AD.
依题意tan∠CAD=![]() .
.
因为AD=1,所以CD=![]() .
.
设AB=x(x>0),则BD=![]() .
.
依题意△ABD∽△DCB,所以![]() ,
,
即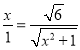 ,解得x=
,解得x=![]() ,
,
故AB=![]() ,BD=
,BD=![]() ,BC=
,BC=![]()
以D为坐标原点,射线DB,DC分别为x轴,y轴的正半轴,
建立如图所示的空间直角坐标系Dxyz,
则D(0,0,0),B(![]() ,0,0),C(0,
,0,0),C(0,![]() ,0),
,0),
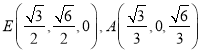
所以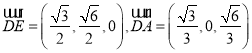 .
.
平面BAD的一个法向量![]() =(0,1,0).
=(0,1,0).
设平面ADE的法向量为![]() =(x,y,z),
=(x,y,z),
由![]() 得,
得,
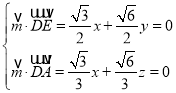
令x=![]() ,得y=-
,得y=-![]() ,z=-
,z=-![]() ,
,
所以![]() 为平面ADE的一个法向量.
为平面ADE的一个法向量.
所以![]() .
.![]()
由图可知二面角BADE的平面角为锐角,
所以二面角BADE的余弦值为![]() .
.

练习册系列答案
相关题目