题目内容
已知函数 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为 ,且过点
,且过点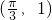 .
.
(I)函数f(x)的达式;
(Ⅱ)在△ABC中.a、b、c分别是角A、B、C的对边,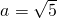 ,
,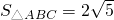 ,角C为锐角.且满
,角C为锐角.且满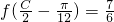 ,求c的值.
,求c的值.
解:(I)∵ =
= sin(ωx+φ),
sin(ωx+φ), =
= [1-cos(ωx+φ)]
[1-cos(ωx+φ)]
∴
= sin(ωx+φ)+
sin(ωx+φ)+ [1-cos(ωx+φ)]=sin(ωx+φ-
[1-cos(ωx+φ)]=sin(ωx+φ- )+
)+
∵函数图象的两个相邻对称中心的距离为 ,∴函数的周期T=
,∴函数的周期T= =π,得ω=2
=π,得ω=2
∵点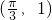 是函数图象上的点,
是函数图象上的点,
∴f( )=sin(2×
)=sin(2× +φ+
+φ+ )+
)+ =1,解之得cosφ=
=1,解之得cosφ=
∵φ∈(0, ),∴φ=
),∴φ=
因此,函数f(x)的达式为f(x)=sin(2x- )+
)+ ;
;
(II)f( -
- )=sin(C-
)=sin(C- +
+ )+
)+ =
= ,解之得sinC=
,解之得sinC=
∵0<C< ,∴cosC=
,∴cosC= =
=
又∵a= ,S△ABC=2
,S△ABC=2
∴ ×a×b×sinC=2
×a×b×sinC=2 ,即
,即 ×
× ×b×
×b× =2
=2 ,解之得b=6
,解之得b=6
根据余弦定理,得c2=a2+b2-2abcosC=5+36-2× ×6×
×6× =21
=21
∴c= ,即得c的值为
,即得c的值为 .
.
分析:(I)由二倍角的三角函数公式和辅助角公式,化简得f(x)=sin(ωx+φ- )+
)+ ,结合图象的两个相邻对称中心的距离为
,结合图象的两个相邻对称中心的距离为 和点
和点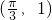 在函数图象上,建立关于ω、φ的关系式,解之即可得到函数f(x)的达式;
在函数图象上,建立关于ω、φ的关系式,解之即可得到函数f(x)的达式;
(II)将 代入函数表达式,解出sinC=
代入函数表达式,解出sinC= ,结合C为锐角,算出cosC=
,结合C为锐角,算出cosC= .根据面积正弦定理公式,由S△ABC=2
.根据面积正弦定理公式,由S△ABC=2 算出b=6,最后由余弦定理代入题中的数据即可求出边c的值.
算出b=6,最后由余弦定理代入题中的数据即可求出边c的值.
点评:本题给出三角函数式,根据函数的图象特征求函数表达式,并依此解三角形ABC的边c的长,着重考查了三角恒等变换、正余弦定理和三角函数的图象与性质等知识,属于基础题.
 =
= sin(ωx+φ),
sin(ωx+φ), =
= [1-cos(ωx+φ)]
[1-cos(ωx+φ)]∴

=
 sin(ωx+φ)+
sin(ωx+φ)+ [1-cos(ωx+φ)]=sin(ωx+φ-
[1-cos(ωx+φ)]=sin(ωx+φ- )+
)+
∵函数图象的两个相邻对称中心的距离为
 ,∴函数的周期T=
,∴函数的周期T= =π,得ω=2
=π,得ω=2∵点
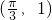 是函数图象上的点,
是函数图象上的点,∴f(
 )=sin(2×
)=sin(2× +φ+
+φ+ )+
)+ =1,解之得cosφ=
=1,解之得cosφ=
∵φ∈(0,
 ),∴φ=
),∴φ=
因此,函数f(x)的达式为f(x)=sin(2x-
 )+
)+ ;
;(II)f(
 -
- )=sin(C-
)=sin(C- +
+ )+
)+ =
= ,解之得sinC=
,解之得sinC=
∵0<C<
 ,∴cosC=
,∴cosC= =
=
又∵a=
 ,S△ABC=2
,S△ABC=2
∴
 ×a×b×sinC=2
×a×b×sinC=2 ,即
,即 ×
× ×b×
×b× =2
=2 ,解之得b=6
,解之得b=6根据余弦定理,得c2=a2+b2-2abcosC=5+36-2×
 ×6×
×6× =21
=21∴c=
 ,即得c的值为
,即得c的值为 .
.分析:(I)由二倍角的三角函数公式和辅助角公式,化简得f(x)=sin(ωx+φ-
 )+
)+ ,结合图象的两个相邻对称中心的距离为
,结合图象的两个相邻对称中心的距离为 和点
和点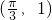 在函数图象上,建立关于ω、φ的关系式,解之即可得到函数f(x)的达式;
在函数图象上,建立关于ω、φ的关系式,解之即可得到函数f(x)的达式;(II)将
 代入函数表达式,解出sinC=
代入函数表达式,解出sinC= ,结合C为锐角,算出cosC=
,结合C为锐角,算出cosC= .根据面积正弦定理公式,由S△ABC=2
.根据面积正弦定理公式,由S△ABC=2 算出b=6,最后由余弦定理代入题中的数据即可求出边c的值.
算出b=6,最后由余弦定理代入题中的数据即可求出边c的值.点评:本题给出三角函数式,根据函数的图象特征求函数表达式,并依此解三角形ABC的边c的长,着重考查了三角恒等变换、正余弦定理和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
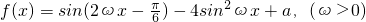 ,其图象的相邻两个最高点之间的距离为π,
,其图象的相邻两个最高点之间的距离为π, 上的最小值为
上的最小值为 ,求函数f(x),(x∈R)的值域.
,求函数f(x),(x∈R)的值域. .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为 ,且过点
,且过点 .
. 的达式;
的达式; ,
,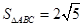 ,角C为锐角。且满
,角C为锐角。且满 ,求c的值.
,求c的值.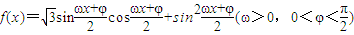 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为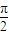 ,且过点
,且过点 .
.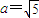 ,
,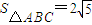 ,角C为锐角.且满
,角C为锐角.且满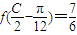 ,求c的值.
,求c的值. .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为 ,且过点
,且过点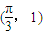 .
. ,
,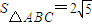 ,角C为锐角.且满
,角C为锐角.且满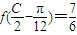 ,求c的值.
,求c的值.