题目内容
设数列{an}的前n项和为Sn,已知a1=8,an+1=Sn+3n+1+5,n∈N*。
(1)设bn=an-2·3n,证明:数列{bn}是等比数列;
(2)证明: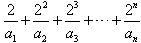 <1。
<1。
(1)设bn=an-2·3n,证明:数列{bn}是等比数列;
(2)证明:
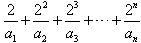 <1。
<1。解:(1)∵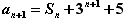
∴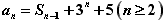
∴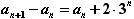
即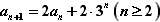
当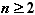 时,
时,
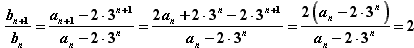
又∵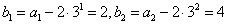
∴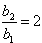
∴数列{bn}是以2为首项,公比为2的等比数列;
(2)由(1)知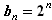
∴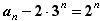
∴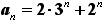
∵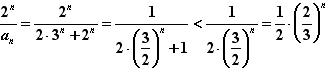
∴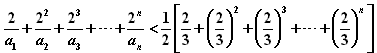
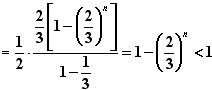 。
。
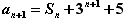
∴
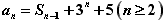
∴
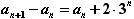
即
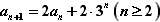
当
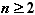 时,
时,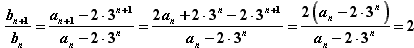
又∵
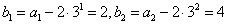
∴
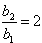
∴数列{bn}是以2为首项,公比为2的等比数列;
(2)由(1)知
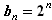
∴
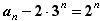
∴
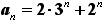
∵
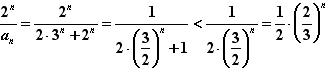
∴
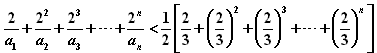
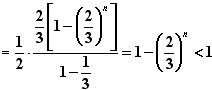 。
。
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目