题目内容
已知数集序列{1},{3,5},{7,9,11},{13,15,17,19},…，其中第n个集合中有n个元素(n∈N*),每一个集合都由连续正奇数组成,并且每一个集合中的最大数与后一个集合中的最小数是连续奇数.(1)求数集序列第n个集合中最大数an的表达式;
(2)设数集序列第n个集合中各数之和为Tn.
①求Tn的表达式;
②令f(n)=(
)n,求证:2≤f(n)＜3.
解:(1)∵第n个集合有n个奇数,
∴在前n个集合中共有奇数的个数为1+2+3+…+(n-1)+n=n(n+1).
则第n个集合中最大的奇数an=2×
n(n+1)-1=n2+n-1.
(2)①由(1)得an=n2+n-1,
从而得Tn=n(n2+n-1)-
×2=n3.
②由①得Tn=n3,
∴f(n)=(1+
)n=(1+
)n(n∈N*).
ⅰ当n=1时,f(1)=2,显然2≤f(1)＜3.
ⅱ当n≥2时,(1+
)n=
(
)0+
(
)1+
(
)2+…+
(
)n
＞
(
)0+
(
)1=2,
(
)k=
·
＜
≤
=
-
.
∴(1+
)n=
(
)0+
(
)1+
(
)2+…+
(
)n
＜1+1+(1-
)+(
-
)+…+(
-
)
=3-
＜3,
即2＜f(n)＜3.
综上所述,2≤f(n)＜3.
练习册系列答案
相关题目
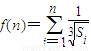，求证：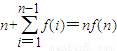
．