题目内容
已知数列{an}满足a1=1,an+1=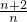 an+1(n∈N*).
an+1(n∈N*).
(1)证明数列{ }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)设bn= ,求证:b1+b2+…+bn<6.
,求证:b1+b2+…+bn<6.
(1)证明:∵an+1=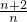 an+1,∴an=
an+1,∴an= an-1+1
an-1+1
两式相减可得an+1-an=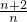 an-
an- an-1,
an-1,
整理可得 ,
,
∴数列{ }是等差数列;
}是等差数列;
(2)解:∵a1=1,an+1=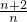 an+1,∴a2=3a1+1=4
an+1,∴a2=3a1+1=4
∴
∴数列{ }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
∴ =n,
=n,
∴an=n2;
(3)证明:n≥2时,bn= =
= =
= <
< =4(
=4( )
)
∴b1+b2+…+bn<b1+4[(1- )+(
)+( )+…+(
)+…+( )=2+4(
)=2+4( )<6.
)<6.
分析:(1)根据数列递推式,再写一式,两式相减整理可得 ,即可得到数列{
,即可得到数列{ }是等差数列;
}是等差数列;
(2)确定数列{ }是以1为首项,1为公差的等差数列,即可求数列{an}的通项公式;
}是以1为首项,1为公差的等差数列,即可求数列{an}的通项公式;
(3)对通项放缩,再裂项求和,即可证得结论.
点评:本题考查数列递推式,考查数列的通项,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
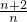 an+1,∴an=
an+1,∴an= an-1+1
an-1+1两式相减可得an+1-an=
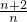 an-
an- an-1,
an-1,整理可得
 ,
,∴数列{
 }是等差数列;
}是等差数列;(2)解:∵a1=1,an+1=
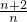 an+1,∴a2=3a1+1=4
an+1,∴a2=3a1+1=4∴

∴数列{
 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列∴
 =n,
=n,∴an=n2;
(3)证明:n≥2时,bn=
 =
= =
= <
< =4(
=4( )
)∴b1+b2+…+bn<b1+4[(1-
 )+(
)+( )+…+(
)+…+( )=2+4(
)=2+4( )<6.
)<6.分析:(1)根据数列递推式,再写一式,两式相减整理可得
 ,即可得到数列{
,即可得到数列{ }是等差数列;
}是等差数列;(2)确定数列{
 }是以1为首项,1为公差的等差数列,即可求数列{an}的通项公式;
}是以1为首项,1为公差的等差数列,即可求数列{an}的通项公式;(3)对通项放缩,再裂项求和,即可证得结论.
点评:本题考查数列递推式,考查数列的通项,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目