题目内容
请先阅读:在等式cos2x=2cos2x-1 (x∈R)的两边对x求导(cos2x)′=(2cos2x-1)′,由求导法则得(-sin2x)·2=4cosx(-sinx),化简后得等式sin2x=2sinxcosx,
(Ⅰ)利用上述想法(或者其他方法),试由等式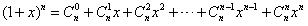 (x∈R,整数n≥2),证明:
(x∈R,整数n≥2),证明: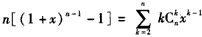 ;
;
(Ⅱ)对于整数n≥3,求证:
(ⅰ)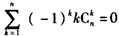 ;
;
(ⅱ)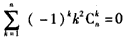 ;
;
(ⅲ)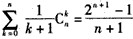 。
。
(Ⅰ)利用上述想法(或者其他方法),试由等式
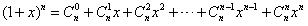 (x∈R,整数n≥2),证明:
(x∈R,整数n≥2),证明: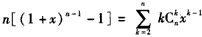 ;
;(Ⅱ)对于整数n≥3,求证:
(ⅰ)
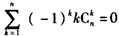 ;
;(ⅱ)
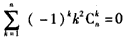 ;
;(ⅲ)
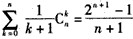 。
。 证明:(Ⅰ)在等式 两边对x求导,得
两边对x求导,得

 ,
,
移项得 。(*)
。(*)
(Ⅱ)(ⅰ)在(*)式中,令x=-1,
整理,得 ,
,
所以 。
。
(ⅱ)由(Ⅰ)知
 ,
,
两边对x求导,得
 ,
,
在上式中令x= -1,得 ,
,
即 ,
,
亦即 ,①
,①
又由(ⅰ)知, ,②
,②
由①+②,得 。
。
(ⅲ)将等式 两边在[0,1]上对x积分,
两边在[0,1]上对x积分,
 ,
,
由微积分基本定理,得
 ,
,
所以 。
。
 两边对x求导,得
两边对x求导,得
 ,
,移项得
 。(*)
。(*)(Ⅱ)(ⅰ)在(*)式中,令x=-1,
整理,得
 ,
,所以
 。
。(ⅱ)由(Ⅰ)知

 ,
,两边对x求导,得

 ,
,在上式中令x= -1,得
 ,
,即
 ,
,亦即
 ,①
,①又由(ⅰ)知,
 ,②
,②由①+②,得
 。
。(ⅲ)将等式
 两边在[0,1]上对x积分,
两边在[0,1]上对x积分, ,
,由微积分基本定理,得
 ,
,所以
 。
。
练习册系列答案
相关题目

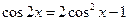 (
(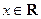 )的两边求导,得:
)的两边求导,得: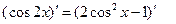 ,
, ,化简得等式:
,化简得等式: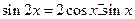 。
。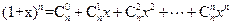 (
(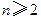 ),证明:
),证明: 。
。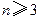 ,求证:
,求证: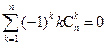 ; (ii)
; (ii)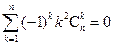 ; (iii)
; (iii)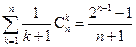 。
。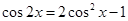 (
(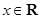 )的两边求导,得:
)的两边求导,得: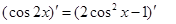 ,
,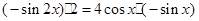 ,化简得等式:
,化简得等式: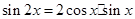 。
。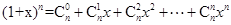 (
(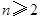 ),证明:
),证明: 。
。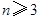 ,求证:
,求证: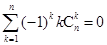 ; (ii)
; (ii)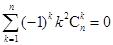 ; (iii)
; (iii)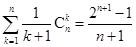 。
。