题目内容

15．在△ABC中，若cosAcosBcosC＜0，则△ABC是（　　）
A．锐角三角形B．直角三角形
C．钝角三角形D．锐角或钝角三角形

分析 根据余弦函数在（0，π）上的性质进行判断即可．

解答 解：∵在△ABC中，若cosAcosBcosC＜0，
∴在△ABC中，cosA，cosB，cosC，必有一个小于0，
部分假设cosA＜0，
则$\frac{π}{2}$＜A＜π，
即△ABC是钝角三角形，
故选：C

点评 本题主要考查三角形性状的判断，根据余弦函数的符号是解决本题的关键．

练习册系列答案
相关题目
5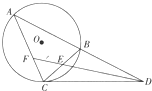．如图所示，已知A、B、C三点都在⊙O上，CD是⊙O的切线，直线AB与CD交于点D．
（Ⅰ）若∠ADC的平分线分别交BC、AC于点E、F，求证：CE=CF；
（Ⅱ）若CD=6，BC=5，求线段AC的长．
6．已知双曲线Γ：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F，以原点为圆心，OF为半径的圆分别与双曲线Γ的一条渐近线及双曲线Γ交于M、N两点（其中M、N均为第一象限上的点），当MF∥ON时，双曲线Γ的离心离一定在区间（　　）
A．（1，$\frac{4}{3}$）B．（$\frac{4}{3}$，$\sqrt{2}$）C．（$\sqrt{2}$，$\sqrt{3}$）D．（$\sqrt{3}$，2）
3．已知数列{an}满足：a1=2，an=an-1+2n（n≥2）
（1）求数列{an}的通项an
（2）求数列{an}的前n项和Sn．
10．若函数f（x）的定义域是（-1，0），则函数f（sinx）的定义域是（2kπ-π，2kπ），k∈Z．
20．把6位同学平均分成3组，每组2人，则共有多少种不同分组法？
7．已知正△ABC边长为1，P在内部（不含边界）任意点，设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$（x，y∈R），则在坐标系中点（x，y）对应区域面积为$\frac{1}{2}$．
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$，F（1，0），是椭圆C的右焦点，若不经过原点O的直线l：y=kx+m（k＞0）与椭圆C相交于不同的两点A、B，记直线OA，OB的斜率分别为k1，k2，且k1•k2=k2．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求证：直线AB的斜率为定值，并求△AOB面积的最大值．
10．三棱锥S-ABC的三视图如图，若点S，A，B，C都在球O的球面上，则球O的表面积是（　　）
A．4πB．8πC．12πD．15π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网