题目内容
如图,在四棱锥P-ABCD中,底面ABCD为菱形,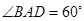 ,Q为AD的中点.
,Q为AD的中点.

(1)若PA=PD,求证:平面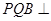 平面PAD;
平面PAD;
(2)点M在线段上,PM=tPC,试确定实数t的值,使PA//平面MQB.
(1)见解析(2)
解析试题分析:
(1)要证明平面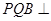 平面PAD,根据面面垂直的定义,只需要在面PAD中找到一条直线AD垂直于面PQB即可,根据三角形PAD为等腰三角形且Q为中点,三线合一即可得到PQ垂直于AD,再利用底面四边形ABCD为菱形且有个角为60度即可得到三星ABD为等边三角形,再次利用等腰三角形的三线合一即可证明QB垂直于AD,则AD垂直于面PQB内两条相交的线段QB与PQ,即可得到AD垂直于面PQB,即有面面垂直.
平面PAD,根据面面垂直的定义,只需要在面PAD中找到一条直线AD垂直于面PQB即可,根据三角形PAD为等腰三角形且Q为中点,三线合一即可得到PQ垂直于AD,再利用底面四边形ABCD为菱形且有个角为60度即可得到三星ABD为等边三角形,再次利用等腰三角形的三线合一即可证明QB垂直于AD,则AD垂直于面PQB内两条相交的线段QB与PQ,即可得到AD垂直于面PQB,即有面面垂直.
(2)连 交
交 于
于 ,根据线面平行的性质定理,可以得到
,根据线面平行的性质定理,可以得到 ,则在三角形PAC与三角形MNC中,有一组边平行,则两个三角形相似,则有
,则在三角形PAC与三角形MNC中,有一组边平行,则两个三角形相似,则有 ,利用底面是有个角为60度的菱形和Q为中点可以求的
,利用底面是有个角为60度的菱形和Q为中点可以求的 ,即可得到
,即可得到 .
.
试题解析:
(1)连结 ,因为四边形
,因为四边形 为菱形,
为菱形,
且 ,所以
,所以 为正三角形,
为正三角形,
又 为
为 的中点,所以
的中点,所以 ; 2分
; 2分
又因为 ,Q为AD的中点,所以
,Q为AD的中点,所以 .
.
又 ,所以
,所以 4分
4分
又 ,所以
,所以 6分
6分
(2)证明:因为 平面
平面 ,连
,连 交
交 于
于 ,
,
由 可得,
可得, ∽
∽ ,所以
,所以 , 8分
, 8分
因为 平面
平面 ,
, 平面
平面 ,平面
,平面
 平面
平面
 .
.
所以 , 10分
, 10分
因此, .即
.即 的值为
的值为 . 12分
. 12分

考点:线面平行的性质定理面面垂直三线合一

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.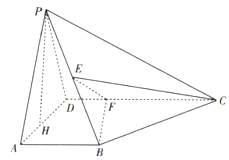
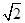 ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;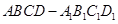 中,已知
中,已知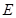 为棱
为棱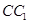 上的动点.
上的动点.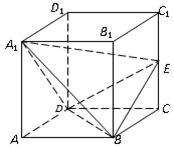
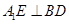 ;
;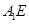 与平面
与平面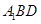 所成角的正弦值.
所成角的正弦值.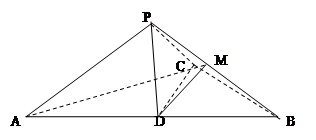 .
.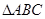 在平面
在平面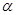 内,
内,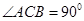 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面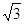 ,
,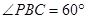
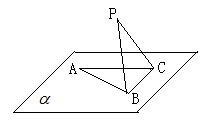
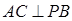
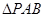 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
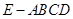 ,底面
,底面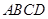 是矩形,平面
是矩形,平面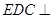 底面
底面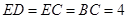 ,
,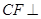 平面
平面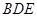 ,且点
,且点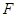 在
在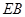 上.
上.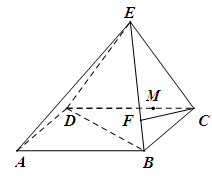
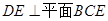 ;
;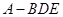 的体积;
的体积;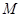 在线段
在线段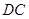 上,且满足
上,且满足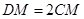 ,试在线段
,试在线段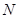 ,使得
,使得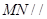 平面
平面 .
. ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
