题目内容
已知函数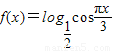
，函数
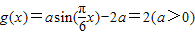，x∈（0，1），若存在x1，x2∈（0，1），使得f（x1）=g（x2）成立，则实数a的取值范围是（ ）A．（
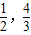）B．
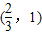
C．
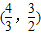
D．（
，
）
【答案】分析：先由条件求得f（x）的值域，函数g（x）的值域，再根据这两个函数的值域的交集非空，求得a的范围．
解答：解：由于x∈（0，1），可得f（x）的值域为（0，1），
函数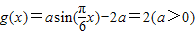
的值域为（2-2a，2-
），
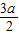由于存在x1，x2∈（0，1），使得f（x1）=g（x2）成立，故（0，1）∩（2-2a，2-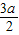
）≠∅，
若（0，1）∩（2-2a，2-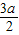
）=∅，则有2-2a≥1，或 2-
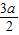≤0．
解得 a≤
，或a≥
，故a的范围为（
，
）．
点评：本题主要考查复合三角函数的单调性，体现了转化的数学思想，属于中档题．
解答：解：由于x∈（0，1），可得f（x）的值域为（0，1），
函数
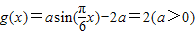的值域为（2-2a，2-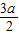），由于存在x1，x2∈（0，1），使得f（x1）=g（x2）成立，故（0，1）∩（2-2a，2-
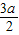）≠∅，若（0，1）∩（2-2a，2-
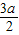）=∅，则有2-2a≥1，或 2-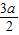≤0．解得 a≤
，或a≥，故a的范围为（，）．点评：本题主要考查复合三角函数的单调性，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
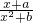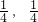是定义在R上的奇函数，其值域为[-
]．
是定义在R上的奇函数，其值域为[-
]．