题目内容
已知数列 满足:
满足: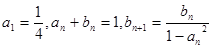
1)求 的值; 2)求证数列
的值; 2)求证数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
3)设 若
若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
解:(1) ∵ ∴
∴
(2) ; (3)
; (3)  .
.
【解析】第一问中,利用 ,递推关系得到,
,递推关系得到,
∵ ∴
∴
第二问中,∵ ∴
∴
∴数列{ }是以-4为首项,-1为公差的等差数列。∴
}是以-4为首项,-1为公差的等差数列。∴
第三问中, ……………8分
……………8分
∴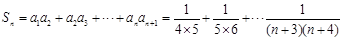
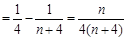
∴
由条件可知 恒成立即可满足条件
恒成立即可满足条件
解:(1) 
∵ ∴
∴ ……………3分
……………3分
(2)∵ ∴
∴
∴数列{ }是以-4为首项,-1为公差的等差数列。
……………5分
}是以-4为首项,-1为公差的等差数列。
……………5分
∴ ∴
∴ ……………7分
……………7分
(3) ……………8分
……………8分
∴
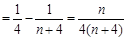 ……………9分
……………9分
∴ ……………10分
……………10分
由条件可知 恒成立即可满足条件
恒成立即可满足条件
设 ……………11分
……………11分
 时,
时,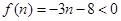 恒成立, ∴
恒成立, ∴ 可取;
可取;
 时,由二次函数的性质知不可能成立;∴
时,由二次函数的性质知不可能成立;∴ 不可取;
不可取;
 时,对称轴
时,对称轴
 在
在 为单调递减函数.
故只要
为单调递减函数.
故只要 即可,
即可,
由
得  ∴
∴ 时
时 恒成立
……………13分
恒成立
……………13分
综上知:实数 的取值范围为
的取值范围为 .
……………14分
.
……………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,
, ;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和
;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和 。
。 满足
满足 ,
, ,求
,求 ;
; ,使当
,使当 时,
时, ,否则说明理由;
,否则说明理由; }满足
}满足 .
. }满足
}满足 ,设
,设 是数列
是数列 的前n项和.
的前n项和.