Question

如图,四棱锥P—ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点.

(1)求证:平面PDC⊥平面PAD;

(2)求证:BE∥平面PAD;

(3)假定PA=AD=CD,求二面角E-BD-C的平面角的正切值.

Answer 1

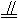
(1)证明:∵PA⊥面ABCD,

∴PA⊥DC.?

∵DC⊥AD且AD∩PA=A,?

∴DC⊥面PAD.?

∵DC面PDC,?

∴平面PDC⊥平面PAD.                                                                                         ?

(2)证明:取PD中点F，连结EF、FA.?

∵E为PC中点，∴在△PDC中,EFDC.?

∴EFAB.?

∴四边形ABEF为平行四边形，即BE∥AF.?

∵AF面PAD且BE面PAD,?

∴BE∥平面PAD.                                                                                                   ?

(3)解:连结AC，取AC中点O，连接EO.?

在△PAC中,EOPA,?

∴EO⊥面ABC.?

过O作OG⊥BD交BD于G，连结EG.?

由三垂线定理知∠EGO为所求二面角E-BD-C的平面角.                                                ?

设PA=AD=CD=2a,AB=a,∴EO=a.?

连结DO并延长交AB于B′，则四边形AB′CD为正方形，且B′B=a,O为DB′中点，过B′作B′G′⊥DB交BD于G′.?

∴OG=B′G′=BB′·sin∠B′BG′=BB′·sin∠ABD?

=a·=a=a.?

在△EOG中,tan∠EGO===.                                                             ?

故二面角E-BD-C的平面角的正切值为.