题目内容
设实数x,y满足条件 ,则
,则 的取值范围为________.
的取值范围为________.
[-4,3]
分析:利用待定系数法表示出 ,再结合
,再结合 ,即可求得取值范围.
,即可求得取值范围.
解答:设 =alg(xy2)+b
=alg(xy2)+b ,则3lgx-4lgy=(a+2b)x+(2a-b)y
,则3lgx-4lgy=(a+2b)x+(2a-b)y
∴ ,∴
,∴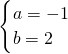
∴
∵
∴-4≤ ≤3
≤3
故答案为:[-4,3]
点评:本题主要考查不等式的基本性质和等价转化思想,考查学生的计算能力,属于中档题.
分析:利用待定系数法表示出
 ,再结合
,再结合 ,即可求得取值范围.
,即可求得取值范围.解答:设
 =alg(xy2)+b
=alg(xy2)+b ,则3lgx-4lgy=(a+2b)x+(2a-b)y
,则3lgx-4lgy=(a+2b)x+(2a-b)y∴
 ,∴
,∴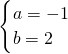
∴

∵

∴-4≤
 ≤3
≤3故答案为:[-4,3]
点评:本题主要考查不等式的基本性质和等价转化思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目