Question

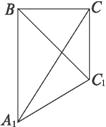
如下图三角形ABC是等腰直角三角形，∠B=90°,D是BC边的中点，BE⊥AD，延长BE交AC于F，连结DF，求证：∠ADB=∠FDC.

Answer 1

思路分析：建立适当的坐标系，利用向量平行和垂直的条件及向量的数量积，转化为证明两向量的夹角相等.

解析：如题图，建立直角坐标系，设A（2，0），C（0，2），则D（0，1），于是=（-2，1），=（-2，2），设F（x,y）,由⊥，得·=0，即（x,y）·(-2,1)=0,

∴-2x+y=0.①

又F点在AC上，则∥.

而=（-x,2-y）,因此2（-x）-(-2)(2-y)=0,

即x+y=2.②

由①②式解得x=,y=,

∴F(,),=(,),=(0,1)·=,

又·=||||cosθ=cosθ,

∴cosθ=,即cos∠FDC=,

又cos∠ADB=,∴cos∠ADB=cos∠FDC,

故∠ADB=∠FDC.

温馨提示

    在解题中要注意题目的隐含条件.如本题中点F满足的关系除了BF⊥AD,还有F点在AC上.点在直线上问题往往转化成两向量共线，利用两向量共线的条件求解.