题目内容
3.4名运动员参加4×100接力赛,根据平时队员训练的成绩,甲不能跑第一棒,乙不能跑第四棒,则不同的出场顺序有( )| A. | 12种 | B. | 14种 | C. | 16种 | D. | 24种 |
分析 分两类,甲跑第四棒和甲不跑第四棒,根据分类计数原理可得
解答 解:甲跑第四棒,则有A33=6种,
甲不跑第四棒,则有C21C21A22=8种,
根据分类计数原理可得共有8+6=14种,
故选:B.
点评 本题考查了分类计数原理,关键是分类,属于基础题

练习册系列答案
相关题目
9.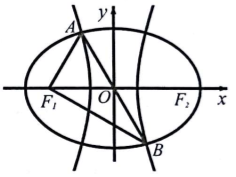 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
11.关于随机对照试验的说法,错误的是( )
| A. | 试验组的对象必须是随机选取的 | |
| B. | 必须有试验组和对照组 | |
| C. | 对照组中的对象不必使用安慰剂 | |
| D. | 在有些随机对照试验中,为了得到更真实的结果,有时还需要使用安慰剂 |
8.过圆x2+y2=25内一点P($\sqrt{15}$,0)作倾斜角互补的直线AC和BD,分别与圆交于A、C和B、D,则四边形ABCD面积的最大值为( )
| A. | 40$\sqrt{3}$ | B. | $\frac{80\sqrt{3}}{3}$ | C. | 40$\sqrt{2}$ | D. | $\frac{80\sqrt{2}}{3}$ |
15.函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2-x)>0的解集为( )
| A. | {x|-2<x<2} | B. | {x|x>2,或x<-2} | C. | {x|0<x<4} | D. | {x|x>4,或x<0} |
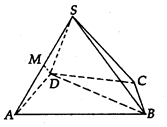 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.