题目内容
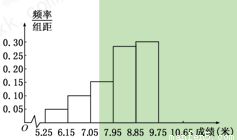
 某市为了了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.1,0.14,0.28,0.3.第6小组的频数是6.
某市为了了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.1,0.14,0.28,0.3.第6小组的频数是6.(Ⅰ)求这次实心球测试成绩合格的人数;
(Ⅱ)经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投一次,求乙投得没有甲远的概率.
分析:(I)第6小组的频率为:1-(0.06+0.10+0.14+0.28+0.30)=0.12,此次测试总人数为
=50人,由此能求出这次实心球测试成绩合格的人数.
(II)设甲、乙各投掷一次的成绩为x,y米,由基本事件满足的区域为
,“乙投得没有甲远”满足的区域为x≥y,由几何概型能求出结果.
| 6 |
| 0.12 |
(II)设甲、乙各投掷一次的成绩为x,y米,由基本事件满足的区域为
|
解答:解:( I)第6小组的频率为1-(0.06+0.10+0.14+0.28+0.30)=0.12
∴此次测试总人数为
=50(人).…(2分)
∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.12)×50=35(人)…(4分)

(Ⅱ)设甲、乙各投掷一次的成绩分别为x、y米,
则基本事件满足的区域为
设事件A为“乙投得没有甲远”满足的区域为x≥y如图所示.
P(A)=
=
…11分
∴乙投得没有甲远的概率为 P(A)=
…12分
∴此次测试总人数为
| 6 |
| 0.12 |
∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.12)×50=35(人)…(4分)

(Ⅱ)设甲、乙各投掷一次的成绩分别为x、y米,
则基本事件满足的区域为
|
设事件A为“乙投得没有甲远”满足的区域为x≥y如图所示.
P(A)=
| ||||||
| 1×2 |
| 1 |
| 16 |
∴乙投得没有甲远的概率为 P(A)=
| 1 |
| 16 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是历年高考的必考题型.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
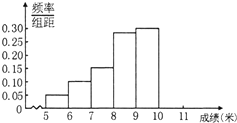
 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7. 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7. 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的 一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的 一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.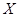 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求