Question

【题目】已知α∈,β∈,cos β=-,sin(α+β)=.

(1)求tan 2β的值;

(2)求α的值.

Answer 1

【答案】（1）；（2）.

【解析】

（1）由已知利用同角三角函数基本关系式可求sinβ，tanβ，再利用二倍角的正切函数公式求解得tan2β的值；（2）由已知可求α+β∈（），利用同角三角函数基本关系式可求cos（α+β），再利用两角差的余弦函数公式可得cosα的值，根据α的范围，从而确定α的值．

(1)因为β∈,cos β=-,可得sin β=,所以tan β=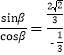=-2,

故tan 2β=.

(2)因为α∈,β∈,所以α+β∈,又因为sin(α+β)=,

所以cos(α+β)=-=-,

于是cos α=cos(α+β-β)=cos(α+β)cos β+sin(α+β)sin β=,

由于α∈,故.