题目内容
若满足条件C=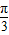 ,AB=
,AB=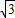 ,BC=a的三角形有两个,则a的取值范围是( )
,BC=a的三角形有两个,则a的取值范围是( )A.(1,2)
B.(
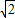 ,
,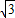 )
)C.(
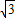 ,2)
,2)D.(1,2)
【答案】分析:由已知条件C的度数,AB及BC的值,根据正弦定理用a表示出sinA,由C的度数及正弦函数的图象可知满足题意△ABC有两个A的范围,然后根据A的范围,利用特殊角的三角函数值即可求出sinA的范围,进而求出a的取值范围.
解答:解:∵C=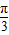 ,AB=
,AB=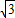 ,BC=a,
,BC=a,
∴由正弦定理得: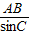 =
=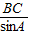 ,即
,即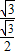 =
=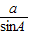 ,
,
解得:sinA=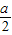 ,
,
由题意得:当A∈(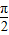 ,
,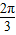 )时,满足条件的△ABC有两个,
)时,满足条件的△ABC有两个,
所以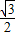 <
<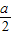 <1,解得:
<1,解得: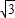 <a<2,
<a<2,
则a的取值范围是(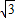 ,2).
,2).
故选C
点评:此题属于解三角形的题型,涉及的知识有:正弦定理,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.
解答:解:∵C=
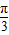 ,AB=
,AB=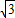 ,BC=a,
,BC=a,∴由正弦定理得:
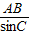 =
=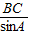 ,即
,即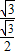 =
=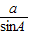 ,
,解得:sinA=
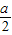 ,
,由题意得:当A∈(
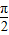 ,
,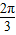 )时,满足条件的△ABC有两个,
)时,满足条件的△ABC有两个,所以
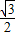 <
<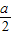 <1,解得:
<1,解得: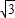 <a<2,
<a<2,则a的取值范围是(
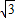 ,2).
,2).故选C
点评:此题属于解三角形的题型,涉及的知识有:正弦定理,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
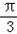 ,AB=
,AB=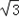 ,BC=a的三角形有两个,则a的取值范围是
,BC=a的三角形有两个,则a的取值范围是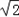 ,
,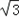 )
)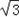 ,2)
,2)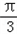 ,AB=
,AB=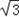 ,BC=a的三角形有两个,则a的取值范围是
,BC=a的三角形有两个,则a的取值范围是 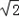 ,
,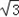 )
)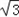 ,2)
,2)