题目内容
已知向量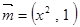 ,
,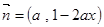 ,其中
,其中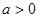 .函数
.函数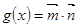 在区间
在区间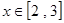 上有最大值为4,设
上有最大值为4,设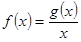 .
.
(1)求实数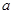 的值;
的值;
(2)若不等式 在
在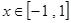 上恒成立,求实数
上恒成立,求实数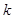 的取值范围.
的取值范围.
(1)1;(2)  .
.
解析试题分析:(1) 通过向量的数量积给出,利用数量积定义求出
通过向量的数量积给出,利用数量积定义求出 ,发现它是二次函数,利用二次函数的单调性可求出
,发现它是二次函数,利用二次函数的单调性可求出 ;(2)由此
;(2)由此 ,不等式
,不等式 在
在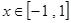 上恒成立,观察这个不等式,可以用换元法令
上恒成立,观察这个不等式,可以用换元法令 ,变形为
,变形为 在
在 时恒成立,从而
时恒成立,从而 ,因此我们只要求出
,因此我们只要求出 的最小值即可.下面我们要看
的最小值即可.下面我们要看 是什么函数,
是什么函数, 可以看作为关于
可以看作为关于 的二次函数,因此问题易解.
的二次函数,因此问题易解.
试题解析:(1)由题得 
又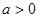 开口向上,对称轴为
开口向上,对称轴为 ,在区间
,在区间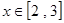 单调递增,最大值为4,
单调递增,最大值为4, 所以,
所以,
(2)由(1)的他,
令 ,则
,则 以
以 可化为
可化为 ,
,
即 恒成立,
恒成立, 且
且 ,当
,当 ,即
,即 时
时 最小值为0,
最小值为0,
考点:(1)二次函数的单调性与最值;(2)换元法与二次函数的最小值.

练习册系列答案
相关题目
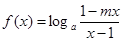 是奇函数,(其中
是奇函数,(其中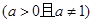 )
)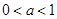 时,讨论函数f(x)的增减性;
时,讨论函数f(x)的增减性; 时,f(x)的值域是(1,
时,f(x)的值域是(1,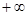 ),求n与a的值。
),求n与a的值。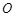 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点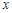 米,圆心角为
米,圆心角为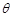 (弧度).
(弧度).
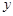 ,求
,求 ,其中
,其中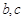 为常数.
为常数.  在区间
在区间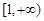 上单调,求
上单调,求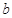 的取值范围;
的取值范围;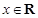 ,都有
,都有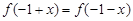 成立,且函数
成立,且函数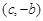 ,
, 满足在集合
满足在集合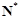 上的值域仍是集合
上的值域仍是集合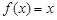 就是N函数.
就是N函数.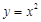 ,②
,②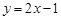 ,③
,③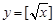 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);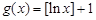 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;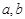 ,函数
,函数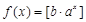 都不是N函数.
都不是N函数. ”表示不超过
”表示不超过 的最大整数)
的最大整数) (单位:千套)与销售价格
(单位:千套)与销售价格 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式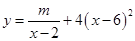 ,其中
,其中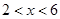 ,
,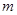 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套. ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式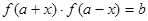 对定义域中的每一个
对定义域中的每一个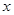 都成立,则称函数
都成立,则称函数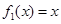 是否为 “(
是否为 “(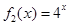 是“(
是“(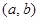 ;,
;, 是“(
是“(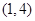 .当
.当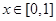 时,
时,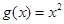
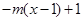
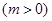 ,若当
,若当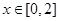 时,都有
时,都有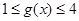 ,试求
,试求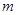 的取值范围.
的取值范围.