题目内容
函数 是
是
- A.非奇非偶函数
- B.仅有最小值的奇函数
- C.仅有最大值的偶函数
- D.既有最大值又有最小值的偶函数
D
分析:利用诱导公式化简解析式,根据奇(偶)的定义判断函数的奇偶性,由倍角公式和配方法整理解析式,根据余弦函数的值域求出函数的最值.
解答: =cos2x+cosx,
=cos2x+cosx,
∴f(-x)=cos(-2x)+cos(-x)=cos2x+cosx=f(x),
∴此函数是偶函数,
∵f(x)=cos2x+cosx=2cos2x+cosx-1=2(cosx+1)2- ,
,
∵cosx∈[-1,1],∴f(x)最大值是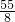 ,最小值是-
,最小值是- .
.
故选D.
点评:本题考查了余弦函数的奇偶性和单调性,利用了诱导公式、倍角公式和配方法整理解析式,最后转化为二次函数求最值,考查了转化思想和知识运用能力.
分析:利用诱导公式化简解析式,根据奇(偶)的定义判断函数的奇偶性,由倍角公式和配方法整理解析式,根据余弦函数的值域求出函数的最值.
解答:
 =cos2x+cosx,
=cos2x+cosx,∴f(-x)=cos(-2x)+cos(-x)=cos2x+cosx=f(x),
∴此函数是偶函数,
∵f(x)=cos2x+cosx=2cos2x+cosx-1=2(cosx+1)2-
 ,
,∵cosx∈[-1,1],∴f(x)最大值是
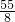 ,最小值是-
,最小值是- .
.故选D.
点评:本题考查了余弦函数的奇偶性和单调性,利用了诱导公式、倍角公式和配方法整理解析式,最后转化为二次函数求最值,考查了转化思想和知识运用能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目