题目内容
已知函数 的图象关于原点对称。
的图象关于原点对称。
(1)求m的值;(2)判断 在
在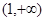 上的单调性,并根据定义证明。
上的单调性,并根据定义证明。
(1)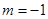 ;(2)当
;(2)当 时,
时,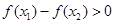 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调增;当
上单调增;当 时,
时,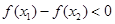 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调减。
上单调减。
解析试题分析:(1)由已知条件得 ------------2分
------------2分
即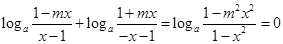 ,
,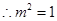 ,即
,即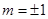 ------2分
------2分
当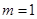 时,
时, 无意义,故
无意义,故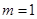 舍去
舍去
因此,只有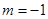 满足题意-----------2分
满足题意-----------2分
(2)由(1)知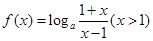 ,设
,设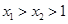
则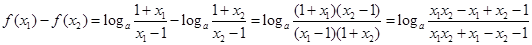
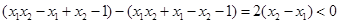 ,且
,且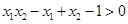 ,
, ,
,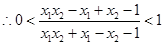 ------------4分
------------4分
当 时,
时,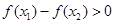 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调增
上单调增
当 时,
时,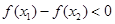 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调减
上单调减
-----------------3分
考点:函数的奇偶性;函数的单调性;用定义法证明函数的单调性。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
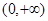 的函数
的函数 ,对任意的
,对任意的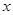 、
、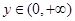 ,都有
,都有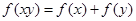 ,且当
,且当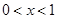 时,
时,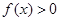 .
.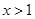 时,
时,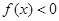 ;
;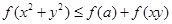 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.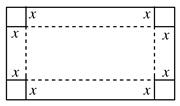
 ,并指出函数
,并指出函数 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值. (1)求函数
(1)求函数 的定义域;
的定义域;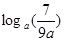 ,求实数
,求实数 的值。
的值。 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为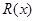 万元,且
万元,且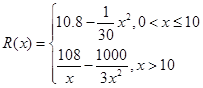 .
.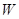 (万元)关于年产量
(万元)关于年产量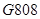 次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程
次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程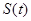 (单位:
(单位: )和时间
)和时间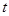 (单位:
(单位: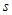 )的关系为:
)的关系为: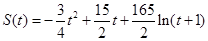 .
. (0<
(0<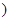 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,则当
,则当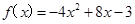 .
.