题目内容
已知f(x)=ax3-2ax2+b(a≠0)。
(1)求出f(x)的极值;
(2)若f(x)在区间[-2,1]上最大值是5,最小值是-11,求f(x)的解析式。
(1)求出f(x)的极值;
(2)若f(x)在区间[-2,1]上最大值是5,最小值是-11,求f(x)的解析式。
解:(1)f'(x)=3ax2-4ax,令 f'(x)=0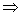 x=0或
x=0或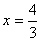
当a>0时
所以当a>0时,x=0时,y取得极大值b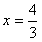 时,y取得极小值
时,y取得极小值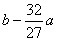
同理当a<0时,x=0时,y取得极小值b,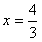 时,y取得极大值
时,y取得极大值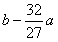 。
。
(2)当a>0时,f(x)在[-2,0)单调递增,在(0,1]单调递减
所以f(x)max=f(0)=b=5
又f(-2)=b-16a<f(1)=b-a,
所以b-16a=-11,a=1
当a<0时,f(x)在[-2,0)单调递减,在(0,1]单调递增,
所以f(x)min= f(0)=b=-11
又f(-2)=b-16a>f(1)=b-a,
所以b-16a=5,a=-1
综上,f(x)=x3-2x2+5或f(x)=-x3+2x2-11。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |