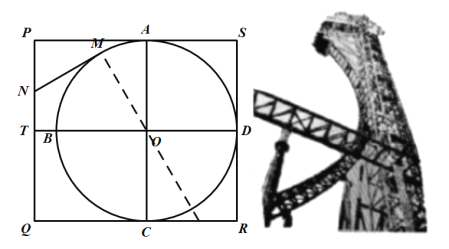
[题目]关于圆周率,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计的值:先请名同学,每人随机写下一个都小于的正实数对,再统计两数能与构成钝角三角形三边的数对的个数;最后再根据统计数m来估计的值.假如统计结果是那么可以估计 . 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】关于圆周率,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计的值:先请名同学,每人随机写下一个都小于的正实数对,再统计两数能与构成钝角三角形三边的数对的个数;最后再根据统计数m来估计的值.假如统计结果是那么可以估计______.

【答案】（或写成3.2）

【解析】

由试验结果知对之间的均匀随机数,对应区域的面积为,两个数能与构成钝角三角形三边的数对,满足且都小,,面积为,由几何概型概率计算公式,得出所取的点在圆内的概率是圆的面积比正方形的面积,二者相等,即可求得答案.

由试验结果知对之间的均匀随机数,对应区域的面积为,两个数能与构成钝角三角形三边的数对,满足且都小,,面积为

又几何概型概率计算公式,得出所取的点在圆内的概率是圆的面积比正方形的面积,二者相等,

统计两数能与构成钝角三角形三边的数对的个数

解题

故答案为:.

练习册系列答案

相关题目

【题目】设函数.

（1）讨论的单调性；

（2）若有两个极值点，，求证：.

【题目】甲、乙两个商场同时出售一款西门子冰箱，其中甲商场位于老城区中心，乙商场位于高新区.为了调查购买者的年龄与购买冰箱的商场选择是否具有相关性，研究人员随机抽取了1000名购买此款冰箱的用户作调研，所得结果如表所示：

	50岁以上	50岁以下
选择甲商场	400	250
选择乙商场	100	250

（1）判断是否有的把握认为购买者的年龄与购买冰箱的商场选择具有相关性；

（2）由于乙商场的销售情况未达到预期标准，商场决定给冰箱的购买者开展返利活动具体方案如下：当天卖出的前60台（含60台）冰箱，每台商家返利200元，卖出60台以上，超出60台的部分，每台返利50元.现将返利活动开展后15天内商场冰箱的销售情况统计如图所示：与此同时，老张得知甲商场也在开展返利活动，其日返利额的平均值为11000元，若老张将选择返利较高的商场购买冰箱，请问老张应当去哪个商场购买冰箱

附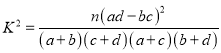：，其中.

	0.100	0.050	0.010	0.001
	2.706	3.841	6.635	10.828

【题目】关于圆周率，数学发展史上出现过许多有创意的求法，如著名的普丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计的值：先请120名同学每人随机写下一个x，y都小于1的正实数对，再统计其中x，y能与1构成钝角三角形三边的数对的个数m，最后根据统计个数m估计的值．如果统计结果是，那么可以估计的值为（）

A.B.C.D.

【题目】某游乐场过山车轨道在同一竖直钢架平面内，如图所示，矩形的长为130米，宽为120米，圆弧形轨道所在圆的圆心为0，圆O与，，分别相切于点A，D，CT为的中点.现欲设计过山车轨道，轨道由五段连接而成：出发点N在线段上（不含端点，游客从点Q处乘升降电梯至点N），轨道第一段与圆O相切于点M，再沿着圆孤轨道到达最高点A，然后在点A处沿垂直轨道急速下降至点O处，接着沿直线轨道滑行至地面点G处（设计要求M，O，G三点共线），最后通过制动装置减速沿水平轨道滑行到达终点R记为，轨道总长度为l米.