题目内容
设函数f(x)= +
+ ,(e为无理数,且e≈2.71828…)是R上的偶函数且a>0.
,(e为无理数,且e≈2.71828…)是R上的偶函数且a>0.
(1)求a的值;
(2)判断f(x)在(0,+∞)上的单调性.
解 (1)∵f(x)是R上的偶函数,∴f(-1)=f(1),∴ +
+ =
= ,即
,即  +
+ =
= +
+ ,即
,即 -
- =
= -ae.
-ae.
∴ =e(
=e(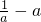 ),∴
),∴ -a=0,∴a2=1.
-a=0,∴a2=1.
又a>0,∴a=1.
(2)由上可得f(x)=ex+e-x.
由于函数f(x)的导数f′(x)=ex- ,当x>0时,ex>1,∴f′(x)=ex-
,当x>0时,ex>1,∴f′(x)=ex- >0,
>0,
∴f(x)在(0,+∞)上为增函数.
分析:(1)由f(x)是R上的偶函数,可得f(-1)=f(1),即 +
+ =
= ,化简得
,化简得  =e(
=e(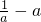 ),故有
),故有 -a=0,a2=1.再由a>0求得a的值.
-a=0,a2=1.再由a>0求得a的值.
(2)由f(x)=ex+e-x,可得函数f(x)的导数f′(x)=ex- ,根据当x>0时,ex>1,可得f′(x)>0,从而得到f(x)在(0,+∞)上为增函数.
,根据当x>0时,ex>1,可得f′(x)>0,从而得到f(x)在(0,+∞)上为增函数.
点评:本题主要考查函数的奇偶性的应用,利用导数判断函数的单调性,属于中档题.
 +
+ =
= ,即
,即  +
+ =
= +
+ ,即
,即 -
- =
= -ae.
-ae.∴
 =e(
=e(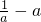 ),∴
),∴ -a=0,∴a2=1.
-a=0,∴a2=1.又a>0,∴a=1.
(2)由上可得f(x)=ex+e-x.
由于函数f(x)的导数f′(x)=ex-
 ,当x>0时,ex>1,∴f′(x)=ex-
,当x>0时,ex>1,∴f′(x)=ex- >0,
>0,∴f(x)在(0,+∞)上为增函数.
分析:(1)由f(x)是R上的偶函数,可得f(-1)=f(1),即
 +
+ =
= ,化简得
,化简得  =e(
=e(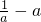 ),故有
),故有 -a=0,a2=1.再由a>0求得a的值.
-a=0,a2=1.再由a>0求得a的值.(2)由f(x)=ex+e-x,可得函数f(x)的导数f′(x)=ex-
 ,根据当x>0时,ex>1,可得f′(x)>0,从而得到f(x)在(0,+∞)上为增函数.
,根据当x>0时,ex>1,可得f′(x)>0,从而得到f(x)在(0,+∞)上为增函数.点评:本题主要考查函数的奇偶性的应用,利用导数判断函数的单调性,属于中档题.

练习册系列答案
相关题目
 (2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
(2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )